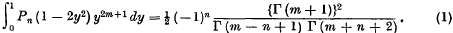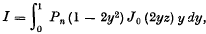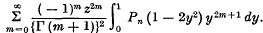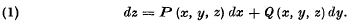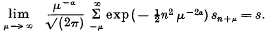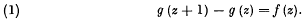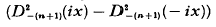Research Article
Congruence Properties of G-Functions
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 61-66
-
- Article
-
- You have access
- Export citation
On Certain Equations to the Cubic Surface, with Extensions to Higher Space
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 1-11
-
- Article
-
- You have access
- Export citation
A special net of quadrics
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 185-209
-
- Article
-
- You have access
- Export citation
On certain new connections between Legendre and Bessel Functions
-
- Published online by Cambridge University Press:
- 20 January 2009, p. 111
-
- Article
-
- You have access
- Export citation
On Vanishing Coaxial Minors
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 210-217
-
- Article
-
- You have access
- Export citation
On the Reduction of Singular Matrix Pencils
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 67-76
-
- Article
-
- You have access
- Export citation
The Absolute Summability (A) of Fourier Series
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 13-17
-
- Article
-
- You have access
- Export citation
An Elementary Proof of the Theorems of Cauchy and Mayer
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 112-117
-
- Article
-
- You have access
- Export citation
On a Theorem of Gauss
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 118-120
-
- Article
-
- You have access
- Export citation
On the Summability of Series by a Method of Valiron
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 218-223
-
- Article
-
- You have access
- Export citation
Note on the “sum” of an integral function
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 77-78
-
- Article
-
- You have access
- Export citation
The Poisson Correlation Function
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 18-26
-
- Article
-
- You have access
- Export citation
The problem of the in-and-circumscribed polygon for a plane quartic curve
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 121-137
-
- Article
-
- You have access
- Export citation
An addendum
-
- Published online by Cambridge University Press:
- 20 January 2009, p. 79
-
- Article
-
- You have access
- Export citation
On the Equivalence of Two Singular Matrix Pencils
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 224-231
-
- Article
-
- You have access
- Export citation
On the squares of Weber's parabolic cylinder functions and certain integrals connected with them
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 27-32
-
- Article
-
- You have access
- Export citation
An Asymptotic Formula for a Class of Distribution Functions
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 138-143
-
- Article
-
- You have access
- Export citation
Some new operational representations
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 232-237
-
- Article
-
- You have access
- Export citation
The Operational Representations of Dn(x) and
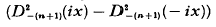
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 33-35
-
- Article
-
- You have access
- Export citation
On a Simple Type of Integro-differential Equation
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 80-84
-
- Article
-
- You have access
- Export citation


 and
and