Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-28T11:33:58.329Z Has data issue: false hasContentIssue false
  • English
  • Français

Note on the “sum” of an integral function

Published online by Cambridge University Press:  20 January 2009

J. M Whittaker
J. M Whittaker
Affiliation:
University of Liverpool
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Theorem 1 of a recent paper “On the asymptotic periods of integral functions” can be replaced by the following more precise result.

If f(z) is an integral function of order ρ there is an integral function g(z), of order ρ, such that

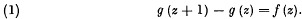
The improvement consists in showing that, if ρ < 1, g (z) can be chosen to be of order ρ, not merely of order less than or equal to one.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 4 , Issue 2 , January 1935 , pp. 77 - 78
Copyright
Copyright © Edinburgh Mathematical Society 1935

References

page 77 note 1 Proc. Edinburgh Math. Soc., 3 (1933), 241–258.CrossRefGoogle Scholar

page 77 note 2 CfNörlund, Sur la “somme” d'une fonction (Paris, 1927), for this and other properties of Bernoulli polynomials.Google Scholar