Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-26T01:07:56.108Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Summability of Series by a Method of Valiron

Published online by Cambridge University Press:  20 January 2009

J. M. Hyslop
J. M. Hyslop
Affiliation:
University of Glasgow.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The method of summability with which I shall be concerned here is denoted by (V, α ) and is defined as follows:—The series Σαn is said to be summable (V, α ) to the sum s if

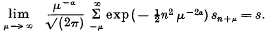
This is a particular case of a method due to Valiron in which μ–2α is replaced by a function of μ.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 4 , Issue 4 , April 1936 , pp. 218 - 223
Copyright
Copyright © Edinburgh Mathematical Society 1936

References

1 Summability (V, α) is usually defined by means of the limit

The definition which I have given makes for greater compactness throughout the paper.

2 Valiron, G., Rendiconti di Palermo, 42 (1917), 267–284.CrossRefGoogle Scholar

3 Hardy, G. H., Quarterly Journal, 35 (1904), 22–66.Google Scholar

4 Valiron, G., loc. cit.Google Scholar

5 Vijayaraghavan, T., Proc. London Math. Soc. (2), 27 (1927–1928), 316–326.Google Scholar

1 Whittaker, E. T. and Watson, G. N., Modern Analysis (1927), 475–476.Google Scholar For a proof of the particular case used above see MacRobert, T. M., Functions of a Complex Variable (1925), 116.Google Scholar

1 Hardy, G. H. and Littlewood, J. E., Annali di Pisa (2), 3 (1934), 54.Google Scholar

2 Vijayaraghavan, T., loc. cit.Google Scholar

3 Valiron, G., loc. cit.Google Scholar

4 Hardy, G. H. and Littlewood, J. E., Rendiconti di Palermo, 41 (1915), 1–18.Google Scholar