In the Euclidean theory of areas, where convex polygons alone are considered, there is no question as to the sign of an area. The element of area is the rectangle, and an area is signless, or always positive.

If by any change of axes ax2 + 2hxy + by2 by changed into a′x′2 + 2h′x′y′ + b′y′2, then will

One of the proofs of the theorem that the three escribed circles and the inscribed circle of a triangle touch a common circle, depends upon the following well-known property of four circles that touch a common circle:—The common tangents of four such circles satisfy the relation

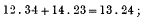
where 12 denotes the common tangent to the circles 1 and 2, etc. The converse part of the theorem, however, namely, that when the above relation holds good, the four circles touch a common circle, is generally assumed; the object of this note is to supply a demonstration of that part of the theorem. It should be noted that if the circles 1 and 2 touch the fifth circle either both externally or both internally, 12 denotes the direct common tangent; while if one of them touches externally and the other internally, 12 denotes the transverse common tangent. Further, the length of the direct common tangent to two circles remains unaltered if the radius of each be diminished or be increased by the same amount; while the length of the transverse common tangent remains unaltered, if the radius of one be increased and that of the other be diminished by the same amount. It is obvious, moreover, that if two circles, 1 and 2, touch a circle A externally, and if the radii of 1 and 2 be diminished and the radius of A increased by the same amount, the contact still holds good; and all the other cases may be easily considered.

The first part of the present paper reproduces an article contributed by me to the July issue of Mathesis, 1900, entitled “Sur les triangles trihomologiques”; the second part contains fresh developments.

It is well known that the properties of the orthocentre and of the nine-point circle of a triangle may be most symmetrically stated when the triangle and its orthocentre are looked upon as the vertices of a four-point, the opposite sides of which intersect at right angles. This point of view leads naturally to a generalisation of the ninepoint circle, by consideration of any four-point in place of the orthic four-point—a generalisation which was first given in detail by Beltrami in the year 1863; though the theorems involved had been previously stated by T. T. Wilkinson. A number of papers have since been written on the nine-point conic; but they have for the most part merely given Beltrami's results over again, and have generally been written in ignorance of his work. In this paper I propose giving the properties of the nine-point conic from a different point of view, associating them with the triangle instead of the four-point. There are certain advantages belonging to each point of view. If, for instance, we consider a triangle ABC with its orthocentre H as an orthic four-point, any proof that shows that the nine-point circle touches the inscribed (or an escribed) circle of the triangle ABC, will, in general, also show that it touches the inscribed (and escribed) circles of the triangles HCB, CHA and BAH. On the other hand, as the nine-point conic circumscribes the diagonal triangle of the four-point, if the four-point is given, the nine-point conic is definitely determined; whereas, if the triangle be considered, as the fourth vertex of the four-point may be taken arbitrarily, a number of nine-point conics are obtained, touching the same inscribed conic.

Suppose possible the relation

where n is an integer and a0, a1, …… an−1, p are rational.

If p is fractional ; then by multiplying throughout by a suitable integer we get a relation of the above form in which all symbols represent integers.

If the original distribution of temperature be symmetrical about the centre, the equation of conduction has the well-known form

with the condition

v being the temperature; and the initial condition gives

The fact that for two or more real positive quantities there exist three well-known algebraic means, the Arithmetic, the Geometric, and the Harmonic, which stand in a fixed order of magnitude independent of the quantities operated on, suggests the question whether there may not be other algebraic means that stand in a definite order of magnitude with reference to those just named and to one another. The following paper supplies an affirmative answer to the question. The results given in the first section are, so far as I know, novel; some of those in the second section are well known, but I hope some freshness may be apparent in their treatment here.

1. If p and q be both commensurable, and if , then, if n be prime to r, both the roots must be commensurable.

For, since n is prime to r, we can find two integers λ and μ such that λn + μr = 1.

1. In Dr Peddie's problem of a sphere cooling in a well-stirred liquid, the conditions to be satisfied by the temperature v(r, t) are

(i) For every positive t, and every r from 0 to a, v is to be finite and one-valued, and is to possess finite derivatives , satisfying

(ii) For every positive t, and r = a,

where p = ⅓ (capacity of liquid)/(capacity of sphere).

(iii) = a given arbitrary function f(r), for every r less than a.

(iv) = initial temperature of liquid = 0 suppose.

1. In attempting some work on geodesics on a spheroid, I was led to work out the geodesic on a sphere, and it may be interesting to see how the usual Spherical Trigonometry results arise from the general equation of a geodesic on a surface of revolution.

In a recent number of the Annals of Mathematics I have shown that the asymptotes of a conic circumscribed about a triangle are isotomic lines with reference to the triangle. By means of this theorem it is easy to find the locus of the centre of a conic, circumscribed about a given triangle, when one of the asymptotes passes through a fixed point.

Let P be any point on a bicircular quartic having A, B, C for foci; so that l. PA + m. PB + n. PC = 0, where l, m, n are known. It will be shown how the fourth focus E (lying upon the circumcircle of ABC) may be found; and also the relations subsisting between any three focal distances.

When the series

is convergent, then Abel's Theorem shows that

Series of the form

are of frequent occurrence in the Analytical Theory of Heat and in other branches of Mathematical Physics, and the conditions to which f(t) is subject usually require that as t tends to zero the function f(t) should tend to the value s.

The problem of the incidence of a train of plane waves on a semi-infinite plane, when the edge of the plane is perpendicular to the direction of the waves, is a two-dimensional one, and was first fully treated in a paper by Sommerfeld. It was also discussed by me in a paper published in the Proceedings of the London Mathematical Society.