1. In Dr Peddie's problem of a sphere cooling in a well-stirred liquid, the conditions to be satisfied by the temperature v(r, t) are

(i) For every positive t, and every r from 0 to a, v is to be finite and one-valued, and is to possess finite derivatives 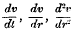, satisfying

(ii) For every positive t, and r = a,

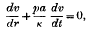
where p = ⅓ (capacity of liquid)/(capacity of sphere).

(iii) 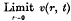= a given arbitrary function f(r), for every r less than a.

(iv) 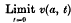= initial temperature of liquid = 0 suppose.