One of the proofs of the theorem that the three escribed circles and the inscribed circle of a triangle touch a common circle, depends upon the following well-known property of four circles that touch a common circle:—The common tangents of four such circles satisfy the relation

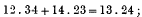
where 12 denotes the common tangent to the circles 1 and 2, etc. The converse part of the theorem, however, namely, that when the above relation holds good, the four circles touch a common circle, is generally assumed; the object of this note is to supply a demonstration of that part of the theorem. It should be noted that if the circles 1 and 2 touch the fifth circle either both externally or both internally, 12 denotes the direct common tangent; while if one of them touches externally and the other internally, 12 denotes the transverse common tangent. Further, the length of the direct common tangent to two circles remains unaltered if the radius of each be diminished or be increased by the same amount; while the length of the transverse common tangent remains unaltered, if the radius of one be increased and that of the other be diminished by the same amount. It is obvious, moreover, that if two circles, 1 and 2, touch a circle A externally, and if the radii of 1 and 2 be diminished and the radius of A increased by the same amount, the contact still holds good; and all the other cases may be easily considered.