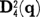If GK is a Chevalley group over a field K of prime characteristic p, the irreducible representations of GK over K form a natural object of study. The basic results have been obtained by Steinberg [15], who showed that, if K is perfect, then each irreducible rational representation of GK over K is a tensor product of representations obtained from certain basic representations by composing them with field automorphisms. These basic representations were obtained by “integrating” the irreducible restricted representations of a restricted Lie algebra associated with the group, which had been studied earlier by Curtis [7]. The present author had obtained the main results previously for the groups SL(n, K), Sp(2n, K) by different means, involving reduction (mod p) from the characteristic 0 case [16]. In this paper we extend this method to the other types of groups, in the hope that some additional insight may be gained.