Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-24T00:04:11.903Z Has data issue: false hasContentIssue false
  • English
  • Français

Singularities of Projective Embedding (Points of order n on an Elliptic Curve)

Published online by Cambridge University Press:  22 January 2016

Akikuni Kato
Akikuni Kato*
Affiliation:
Nagoya Institute for Technology Department of Mathematics
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In the Plücker formula for a curve embedded in a higher dimensional projective space, one encounters the notion of stationary point (cf, [B], [W]). W. F. Pohl gave new view point about it in terms of vector bundles and he defined “the singularities of embedding” (cf. [P]). At first, we shall give dual formulation of Pohl’s one by means of the sheaf of principal parts of order n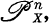, and next we shall prove the following: If an elliptic curve is embedded in (n — l)-dimensional projective space 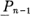as a curve of degree n, singularities of projective embedding of order n — 1 are exactly the points of order n with suitable choice of a neutral element on the curve which is an abelian variety of dimension one. The proof is given by making use of the relation between 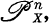and Schwarzenberger’s secant bundle which we shall also give.

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 45 , February 1972 , pp. 97 - 107
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1972

References

[B] Baker, H.F., Principles of geometry Vol. 5.Google Scholar
[EGA] Grothendieck, A., Elements de géométrie algébrique, Publ. Math. IHES.Google Scholar
[P] Pohl, W.F., Differential geometry of higher order, Topology Vol. 1, (1962) 169–211.Google Scholar
[S] Schwarzenberger, R.L.E., The secant bundle of a projective variety, Proc. London Math. Soc. 14 (1964) 369–84.Google Scholar
[W] Weyl, H. and Weyl, J., Meromorphic functions and analytic curves, Ann. Math. No. 12, Princeton Univ. Press. 1943.Google Scholar
[M] Mattuck, A., Secant bundles on symmetric products, Amer. J. of Math. 87 (1965) 779–97.CrossRefGoogle Scholar