One of the most important problems in the potential theory is the one of capacitability, that is, whether the inner capacity of an arbitrary borelian subset B is equal to the outer capacity of B. As for the capacities induced by the Newtonian potentials and other classical potentials, Choquet [5] has shown that every borelian and, more generally, every analytic set are capacitable. He goes on as follows : first he shows that, for the Newtonian capacity f, the inequality of strong subadditivity holds, that is,
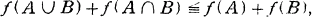
and then, using this inequality, he shows that the outer capacity f* has the analogous property to one of the outer measure, more precisely, if an increasing sequence {An} of arbitrary subsets converges to A, then f*(A) = limf*(An)- This property plays an important role in his proof.