Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-23T23:21:43.115Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Dimension of Modules and Algebras, VIII. Dimension of Tensor Products

Published online by Cambridge University Press:  22 January 2016

Samuel Eilenberg ,
Alex Rosenberg  and
Daniel Zelinsky
Samuel Eilenberg
Affiliation:
Columbia University, Northwestern University and Institute for Advanced Study, Northtvestern University and Kyoto University
Alex Rosenberg
Affiliation:
Columbia University, Northwestern University and Institute for Advanced Study, Northtvestern University and Kyoto University
Daniel Zelinsky
Affiliation:
Columbia University, Northwestern University and Institute for Advanced Study, Northtvestern University and Kyoto University
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

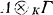The questions concerning the dimension of the tensor product of two K-algebras have turned out to be surprisingly difficult. In this paper we follow a method using spectral sequences (§§1-3) which in some concrete cases yields complete results (§§4-5). In particular, complete results are obtained when r is a ring of matrices, triangular matrices, polynomials or rational functions, so that in the first three cases 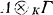is respectively the ring of matrices, triangular matrices or polynomials with coefficients in the arbitrary algebra A.

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 12 , December 1957 , pp. 71 - 93
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1957

References

[ 1 ] Artin, E., Nesbitt, C., and Thrall, R., Rings with minimum condition, University of Michigan Press, Ann Arbor, 1948.Google Scholar
[ 2 ] Auslander, M., On the dimension of modules and algebras, III, Nagoya Math. J., 9 (1955), 67–77.Google Scholar
[ 3 ] Auslander, M., On the dimension of modules and algebras, VI, Nagoya Math. J., 11 (1957), 61–66.Google Scholar
[ 4 ] Eilenberg, S., Algebras of cohomologically finite dimension, Comment. Math. Helv., 28 (1954), 310–319.CrossRefGoogle Scholar
[ 5 ] Eilenberg, S., Ikeda, M., and Nakayama, T., On the dimension of modules and algebras, I, Nagoya Math. J., 8 (1955), 49–57.Google Scholar
[ 6 ] Eilenberg, S., Nagao, H., and Nakayama, T., On the dimension of modules and algebras, IV, Nagoya Math. J., 10 (1956), 87–96.Google Scholar
[ 7 ] Harada, M., Note on the dimension of modules and algebras, J. Inst. Polytech. Osaka City Univ., Ser. A. 7 (1956), 17–27.Google Scholar
[ 8 ] Hochschild, G., On the cohomology groups of an associative algebra, Ann. of Math., 46 (1945), 58–67.Google Scholar
[ 9 ] Hochschild, G., Cohomology and representation of associative algebras, Duke Math. J., 14 (1947), 921–948.CrossRefGoogle Scholar
[10] Rosenberg, A. and Zelinsky, D., Cohomology of infinite algebras, Trans. Amer. Math. Soc., 82 (1956), 85–98.CrossRefGoogle Scholar