We describe the screened Korringa-Kohn-Rostoker (KKR) method and the third-generation linear muffin-tin orbital (LMTO) method for solving the single-particle Schrödinger equation for a MT potential. In the screened KKR method, the eigenvectors CRL,i are given as the non-zero solutions, and the energies εi as those for which such solutions can be found, of the linear homogeneous equations: 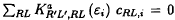 , where Ka (ε) is the screened KKR matrix. The screening is specified by the boundary condition that, when a screened spherical wave
, where Ka (ε) is the screened KKR matrix. The screening is specified by the boundary condition that, when a screened spherical wave 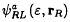 is expanded in spherical harmonics YR′L′ (ȓR′) about its neighboring sites R′, then each component either vanishes at a radius, rR′=aR′L′, or is a regular solution at that site. When the corresponding “hard” spheres are chosen to be nearly touching, then the KKR matrix is usually short ranged and its energy dependence smooth over a range of order 1 Ry around the centre of the valence band. The KKR matrix, K (εν), at a fixed, arbitrary energy turns out to be the negative of the Hamiltonian, and its first energy derivative, K (εν), to be the overlap matrix in a basis of kinked partial waves, φRL (εν, rR), each of which is a partial wave inside the MT-sphere, tailed with a screened spherical wave in the interstitial, or taking the other point of view, a screened spherical wave in the interstitial, augmented by a partial wave inside the sphere. When of short range, K (ε) has the two-centre tight-binding (TB) form and can be generated in real space, simply by inversion of a positive definite matrix for a cluster. The LMTOs, χRL (εν), are smooth orbitals constructed from φRL(εν, rR) and φRL(εν, rR), and the Hamiltonian and overlap matrices in the basis of LMTOs are expressed solely in terms of K (εν) and its first three energy derivatives. The errors of the single-particle energies εi obtained from the Hamiltonian and overlap matrices in the φ(εν)- and χ(εν) bases are respectively of second and fourth order in εi – εi. Third-generation LMTO sets give wave functions which are correct to order εi – εν, not only inside the MT spheres, but also in the interstitial region. As a consequence, the simple and popular formalism which previously resulted from the atomic-spheres approximation (ASA) now holds in general, that is, it includes downfolding and the combined correction. Downfolding to few-orbital, possibly short-ranged, low-energy, and possibly orthonormal Hamiltonians now works exceedingly well, as is demonstrated for a high-temperature superconductor. First-principles sp3 and sp3d5 TB Hamiltonians for the valence and lowest conduction bands of silicon are derived. Finally, we prove that the new method treats overlap of the potential wells correctly to leading order and we demonstrate how this can be exploited to get rid of the empty spheres in the diamond structure.
is expanded in spherical harmonics YR′L′ (ȓR′) about its neighboring sites R′, then each component either vanishes at a radius, rR′=aR′L′, or is a regular solution at that site. When the corresponding “hard” spheres are chosen to be nearly touching, then the KKR matrix is usually short ranged and its energy dependence smooth over a range of order 1 Ry around the centre of the valence band. The KKR matrix, K (εν), at a fixed, arbitrary energy turns out to be the negative of the Hamiltonian, and its first energy derivative, K (εν), to be the overlap matrix in a basis of kinked partial waves, φRL (εν, rR), each of which is a partial wave inside the MT-sphere, tailed with a screened spherical wave in the interstitial, or taking the other point of view, a screened spherical wave in the interstitial, augmented by a partial wave inside the sphere. When of short range, K (ε) has the two-centre tight-binding (TB) form and can be generated in real space, simply by inversion of a positive definite matrix for a cluster. The LMTOs, χRL (εν), are smooth orbitals constructed from φRL(εν, rR) and φRL(εν, rR), and the Hamiltonian and overlap matrices in the basis of LMTOs are expressed solely in terms of K (εν) and its first three energy derivatives. The errors of the single-particle energies εi obtained from the Hamiltonian and overlap matrices in the φ(εν)- and χ(εν) bases are respectively of second and fourth order in εi – εi. Third-generation LMTO sets give wave functions which are correct to order εi – εν, not only inside the MT spheres, but also in the interstitial region. As a consequence, the simple and popular formalism which previously resulted from the atomic-spheres approximation (ASA) now holds in general, that is, it includes downfolding and the combined correction. Downfolding to few-orbital, possibly short-ranged, low-energy, and possibly orthonormal Hamiltonians now works exceedingly well, as is demonstrated for a high-temperature superconductor. First-principles sp3 and sp3d5 TB Hamiltonians for the valence and lowest conduction bands of silicon are derived. Finally, we prove that the new method treats overlap of the potential wells correctly to leading order and we demonstrate how this can be exploited to get rid of the empty spheres in the diamond structure.

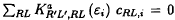 , where
, where 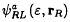 is expanded in spherical harmonics
is expanded in spherical harmonics