Research Article
Order-two density and the strong law of large numbers
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 1-22
-
- Article
- Export citation
Epsilon entropy and the packing of balls in Euclidean space
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 23-31
-
- Article
- Export citation
Simple valuations on convex bodies
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 32-39
-
- Article
- Export citation
Relative norms of prime ideals in small regions
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 40-62
-
- Article
- Export citation
Estimates of hybrid exponential sums on quasiprojective varieties over finite fields
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 63-72
-
- Article
- Export citation
Explicit bounds on exponential sums and the scarcity of squarefree binomial coefficients
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 73-107
-
- Article
- Export citation
Irregularities of distributions with respect to polytopes
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 108-119
-
- Article
- Export citation
On the number of cells defined by a family of polynomials on a variety
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 120-126
-
- Article
- Export citation
The higher Stasheff-Tamari posets
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 127-154
-
- Article
- Export citation
On a question of regarding visibility of lattice points
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 155-158
-
- Article
- Export citation
Bounds on the covering radius of a lattice
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 159-164
-
- Article
- Export citation
Barycentric subdivision of triangles and semigroups of Möbius maps
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 165-171
-
- Article
- Export citation
σ-fragmentability and analyticity
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 172-181
-
- Article
- Export citation
The effect of surface tension on the scattering of waves by a partially immersed vertical barrier in water of infinite depth
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 182-197
-
- Article
- Export citation
Asymptotic theory for a class of fourth-order differential equations
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 198-208
-
- Article
- Export citation
The asymptotic form of the Titchmarsh-weyl m-function associated with a non-definite, linear, second order differential equation
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 209-222
-
- Article
- Export citation
Book Reviews
J. L. Alperin and R. B. Bell. Groups and Representations. Springer.1995, ISBN 0 387 94526 1, 194 pp., Softcover, DM 38. - W. S. Anglin and J. Lambek. The Heritage of Thales. Springer. 1995, ISBN 0 387 94544 X, 327 pp., DM 58. - A. V. Arhangel'skii. Editor. General Topology II. Encyclopaedia of Mathematical Sciences, Vol. 50. Springer. 1995, ISBN 3 540 54695 2, 256 pp., DM 148. - V. I. Arnautov, S. T. Glavatsky and A. V. Mikhalev. Introduction to the Theory of Topological Rings and Modules. Marcel Dekker. 1995, ISBN 0 8247 9323 4, 502 pp., $165. - H. F. Baker. Abelian Functions: Abel's Theorem and the Allied Theory of Theta Functions. New edition, first published in 1897. Cambridge University Press. 1995, ISBN 0 521 49877 5, 684 pp., £27·95. - K. I. Beider, W. S. MartindaleIII and A. V. Mikhalev. Rings with Generalized Identities. Marcel Dekker. 1996, ISBN 0 8247 9325 0, 517 pp., $185. - R. A. Brualdi and B. L. Shader. Matrices of Sign-Solvable Systems. Cambridge Tracts in Mathematics. Cambridge University Press. 1995, ISBN 0 521 48296 8, 298 pp., £30. - H. Cohen. A Course in Computational Algebraic Number Theory. Springer Graduate Texts in Mathematics. Second corrected printing. Springer. 1995, ISBN 3 540 55640 0, 534 pp., £34.50. - P. M. Cohn. Skew Fields. Encyclopaedia of Mathematics and its Applications, Vol. 57. Cambridge University Press. 1995, ISBN 0 521 43217 0, 500 pp., £55. - S. C. Coutinho. A Primer of Algebraic D-modules. LMS Student Texts, 33. Cambridge University Press. 1995, ISBN 0 521 55119 6, 207 pp., £30.00. - P. J. Davis, R. Hersh and E. A. Marchisotto. The Mathematical Experience. Study Edition. Birkhauser. 1995, ISBN 0 8176 3739 7, 487 pp., DM 78. - R. J. Gardner. Geometric Tomography. Cambridge University Press. 1995, ISBN 0 521 45126 4, 424 pp., £45. - I. M. Gelfand, M. M. Kapranov and A. V. Zelevinsky. Discriminants, Resultants and Multidimensional Determinants. Birkhauser. 1994, ISBN 3 7643 3660 9, 523 pp., DM 158. - A. Katok and B. Hasselblatt. Introduction to the Modern Theory of Dynamical Systems. Cambridge University Press. 1995, ISBN 0 521 34187 6, 802 pp., £60. - J. Krajícek. Bounded Arithmetic, Propositional Logic, and Complexity Theory. Cambridge University Press. 1995, ISBN 0 521 45205 8, 343 pp., £40. - J. McCleary. Geometry from a Differentiable Viewpoint. Cambridge University Press. 1994, ISBN 0 521 42480 1, 308 pp., Paperback £14·95. - D. McDuff and D. Salamon. Introduction to Symplectic Topology. Clarendon Press. 1995, ISBN 0 19 851177 9, 425 pp., £45. - C. McLarty. Elementary Categories, Elementary Toposes. Clarendon Press. 1995, ISBN 0 19 851473 5, 265 pp., £25. - R. A. Mollin. Quadratics. CRC Press. 1996, ISBN 0 8493 3983 9, 387 pp., $74.95. - S. P. Novikov. Topology I, General Survey. Encyclopaedia of Mathematical Sciences, Vol. 12. Springer. 1996, ISBN 0 387 17007 3, 319 pp., Hardcover, DM 148. - D. J. S. Robinson. A Course in the Theory of Groups. 2nd Edition. Springer. 1996, ISBN 0 387 94461 3, 499 pp., Hardcover, DM 88. - Sasaki Chikara, Sugiura Mitsuo and J. W. Dauben. Editors. The Intersection of History and Mathematics. Birkhäuser. 1994, ISBN 0 8176 5029 6, 257 pp., £56. - I. R. Shafarevich, Editor. Algebraic Geometry II. Encyclopaedia of Mathematical Sciences, Vol. 35. Springer. 1996, ISBN 3 540 54680 4, 262 pp., Hardcover, DM 148. - J. Thévenaz. G-algebras and Modular Representation Theory. Oxford University Press. 1995, ISBN 0 19 853587 2, 570 pp., £65.
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 223-228
-
- Article
- Export citation
Front matter
MTK volume 43 issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f4
-
- Article
-
- You have access
- Export citation

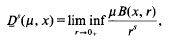
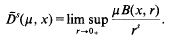
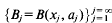 be a sequence of mutually disjoint open balls, with centres
be a sequence of mutually disjoint open balls, with centres 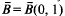 in
in 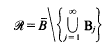
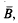 the balls {
the balls {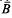 provided that λ(ℛ)=0, where λ denotes the
provided that λ(ℛ)=0, where λ denotes the 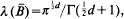 henceforth denoted by
henceforth denoted by 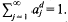 Larman [11] has noted that, under these circumstances, one also has
Larman [11] has noted that, under these circumstances, one also has 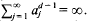 .
.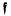 a fixed integral ideal and
a fixed integral ideal and 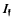 the group of fractional ideals of
the group of fractional ideals of 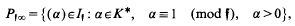
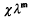 be an arbitrary Groessencharaktere mod f as defined in [15]. Then
be an arbitrary Groessencharaktere mod f as defined in [15]. Then 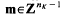 and, for
and, for 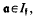
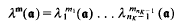
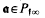 depends only on the
depends only on the 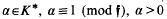 that exists such that
that exists such that 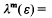 1 for all units ε in
1 for all units ε in 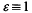 (mod
(mod 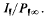
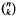 must be highly composite in that it contains many prime factors and often to high powers. It is therefore of interest to enquire as to how infrequently
must be highly composite in that it contains many prime factors and often to high powers. It is therefore of interest to enquire as to how infrequently 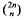 is not squarefree once
is not squarefree once 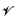 a variety of real dimension
a variety of real dimension 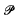 = {
= {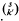 (
(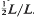 . The convex hull of all minimal vectors of a class
. The convex hull of all minimal vectors of a class 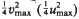 be a maximal squared radius of
be a maximal squared radius of 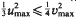 , then
, then 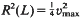 . This is the case in the well-known Barnes-Wall and Leech lattices. Otherwise,
. This is the case in the well-known Barnes-Wall and Leech lattices. Otherwise, 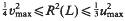 . This is a refinement of a result of Norton ([3], Ch. 22).
. This is a refinement of a result of Norton ([3], Ch. 22).
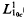 (0, ∞) and λ is a complex number with
(0, ∞) and λ is a complex number with