Article contents
Epsilon entropy and the packing of balls in Euclidean space
Published online by Cambridge University Press: 26 February 2010
Summary
Let 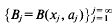 be a sequence of mutually disjoint open balls, with centres xj and corresponding radii aj, each contained in the closed unit ball
be a sequence of mutually disjoint open balls, with centres xj and corresponding radii aj, each contained in the closed unit ball 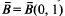 in d-dimensional euclidean space, ℝd. Further we suppose, for simplicity, that the balls Bj are indexed so that aj≥aj+1. The set
in d-dimensional euclidean space, ℝd. Further we suppose, for simplicity, that the balls Bj are indexed so that aj≥aj+1. The set
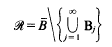
obtained by removing, from 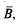 the balls {Bj} is called the residual set. We say that the balls {Bj} constitute a packing of
the balls {Bj} is called the residual set. We say that the balls {Bj} constitute a packing of 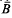 provided that λ(ℛ)=0, where λ denotes the d-dimensional Lebesgue measure. Thus it follows that
provided that λ(ℛ)=0, where λ denotes the d-dimensional Lebesgue measure. Thus it follows that 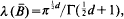 henceforth denoted by c(d), whilst the packing restraint ensures that
henceforth denoted by c(d), whilst the packing restraint ensures that 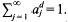 Larman [11] has noted that, under these circumstances, one also has
Larman [11] has noted that, under these circumstances, one also has 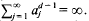 .
.
MSC classification
- Type
- Research Article
- Information
- Copyright
- Copyright © University College London 1996
References
- 1
- Cited by


