Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-16T17:04:36.841Z Has data issue: false hasContentIssue false
  • English
  • Français

Relative norms of prime ideals in small regions

Part of: Algebraic number theory: global fields

Published online by Cambridge University Press:  26 February 2010

M. D. Coleman
M. D. Coleman
Affiliation:
Department of Mathematics, UMIST, P. O. Box 88, Manchester. M60 1QD
Get access

Extract

Let K be a number field of degree nK = r1 + 2r2, 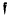a fixed integral ideal and 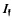the group of fractional ideals of K whose prime decomposition contains no prime factors of 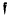. Let

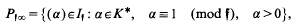
and 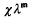be an arbitrary Groessencharaktere mod f as defined in [15]. Then 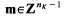and, for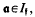

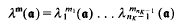
where {λi} forms a basis for the torsion–free characters on 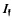whose value on any 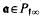depends only on the 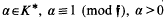that exists such that a = (α). Note that because of the choice in such an α we have that 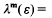1 for all units ε in K satisfying 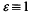(mod 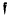), ε>0. Also, x is a narrow ideal class character mod 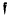, that is, a character on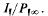

MSC classification

Secondary: 11R44: Distribution of prime ideals
Type
Research Article
Information
Mathematika , Volume 43 , Issue 1 , June 1996 , pp. 40 - 62
Copyright
Copyright © University College London 1996

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Baker, R. C. and Harman, G.. The difference between consecutive primes. To appear.Google Scholar
2.Chandrasekharan, K. and Narasimhan, R.. The approximate functional equation for a class of zeta-functions. Math. Ann., 152 (1963), 30–64.CrossRefGoogle Scholar
3.Cohn, H.. A classical invitation to algebraic numbers and class fields, (Springer-Verlag, 1988).Google Scholar
4.Coleman, M. D.. The distribution of points at which binary quadratic forms are prime. Proc. London Math. Soc. (3), 61 (1990), 433–456.CrossRefGoogle Scholar
5.Coleman, M. D.. A zero-free region for the Hecke L-functions. Mathematika, 37 (1990), 287–304.Google Scholar
6.Coleman, M. D.. The distribution of points at which norm-forms are prime. J. Number Theory, 41 (1992), 359–378.Google Scholar
7.Coleman, M. D.. The Rosser-Iwaniec sieve in number fields which an application. Acta Arith., 65 (1993), 53–83.CrossRefGoogle Scholar
8.Deshouillers, J. M. and Iwaniec, H.. Power mean values of the Riemann zeta-function. Mathematika, 29 (1982), 202–212.Google Scholar
9.Duke, W.. Some problems in multidimensional analytic number theory. Acta Arith., 52 (1989), 203–228.CrossRefGoogle Scholar
10.Lou Shituo, H. Halberstam and Qi, Yao. A new upper bound in the linear sieve. Number Theory, Trace Formulas and Discrete Groups (Academic Press, London, 1989), 331–342.Google Scholar
11.Heath-Brown, D. R.. On the density of zeros of the Dedekind zeta-function. Ada Arith., 33 (1977), 169–181.CrossRefGoogle Scholar
12.Heath-Brown, D. R.. The twelfth power moment of the Riemann zeta-function. Quart. J. Math (Oxford), 29 (1978), 443–462.Google Scholar
13.Heath-Brown, D. R.. Zero density estimates for the Riemann zeta function and Dirichlet L-functions. J. London Math. Soc, 19 (1979), 221–232.Google Scholar
14.Heath-Brown, D. R. and Iwaniec, H.. On the difference between consecutive primes. Invent. Math., 55 (1979), 49–69.CrossRefGoogle Scholar
15.Hecke, E.. Eine neue art von zetafunctionen und ihre beziehung zur verteilung der primzahlen I, II. Math. Z., 1 (1918), 357–376; 6 (1920), 11–51.Google Scholar
16.Huxley, M. N.. The distribution of prime numbers (Oxford University Press, 1972).Google Scholar
17.Ivic, A.. The Riemann zeta-function (John Wiley & Sons, New York, 1985).Google Scholar
18.Iwaniec, H. and Pintz, J.. Primes in short intervals. Montash. Math, 98 (1984), 115–143.Google Scholar
19.Knopfmacher, J.. Abstract analytic number theory (Dover, 1990).Google Scholar
20.Kubilius, J. P.. On a problem in the n-dimensional analytic theory of numbers. Viliniaus Valst. Univ. Mokslo. dardai Fiz. Chem Moksly Ser. 4, (1955), 5–43.Google Scholar
21.Lagarias, J. C. and Odlyzko, A. M.. Effective versions of the Chebotarev density theorem. Algebraic number fields, ed. Frölich, A. (Academic Press, 1977).Google Scholar
22.Lang, S.. Algebraic number theory (Addison-Wesley, 1970).Google Scholar
23.Maknys, M.. On Hecke's z-functions of an algebraic quadratic imaginary number field. Litovsk Mat. Sb., 15 (1975), 157–171.Google Scholar
24.Montgomery, H. L.. Topics in multiplicative number theory. Lecture notes in mathematics, 227 (Springer, Berlin, 1971).CrossRefGoogle Scholar
25.Mozzochi, C. J.. On the difference between consecutive primes. J. Number Theory, 24 (1986), 181–187.CrossRefGoogle Scholar
26.Rademacher, H.. On the Phragmen-Lindelöf theorem and some applications. Math. Z., 72 (1959), 192–204.Google Scholar
27.Ramachandra, K.. A simple proof of the mean fourth power estimates for ζ(½ + it)and L(½+it,x). Ann. Scuola Norm Sup Pisa Cl. Sci. (4), 1 (1974), 81–97.Google Scholar
28.Ricci, S.. Local distribution of primes. PhD. thesis (University of Michigan, 1976).Google Scholar
29.Söhne, P.. An upper bound for Hecke zeta-functions with Groessencharakters. Preprint, University of Marburg.Google Scholar
30.Sokolovsky, A. V.. A theorem on the zeros of Dedekind's zeta-function and the distance between ‘neighbouring’ prime ideals, (Russian). Ada Arith., 13 (1968), 321–334.Google Scholar
31.Tschebotareff, N.. Die bestimmung der Dichtigkeit einer Menge von Primzahlen, welche zu einer gegbenen substitutionsklasse gehören. Math. Ann., 95 (1926), 191–228.Google Scholar
32.Vinogradov, I. M.. The method of trigonometrical sums in the theory of numbers, translated and annotated by Roth, K. F. and Davenport, Anne (Interstate, London, 1954).Google Scholar