No CrossRef data available.
Published online by Cambridge University Press: 26 February 2010
This paper depends on results of Baranovskii [1], [2]. The covering radius R(L) of an n-dimensional lattice L is the radius of smallest balls with centres at points of L which cover the whole space spanned by L. R(L) is closely related to minimal vectors of classes of the quotient 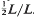 . The convex hull of all minimal vectors of a class Q is a Delaunay polytope P(Q) of dimension ≤, dimension of L. Let
. The convex hull of all minimal vectors of a class Q is a Delaunay polytope P(Q) of dimension ≤, dimension of L. Let 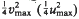 be a maximal squared radius of P(Q) of dimension n (of dimension less than n, respectively). If
be a maximal squared radius of P(Q) of dimension n (of dimension less than n, respectively). If 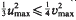 , then
, then 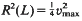 . This is the case in the well-known Barnes-Wall and Leech lattices. Otherwise,
. This is the case in the well-known Barnes-Wall and Leech lattices. Otherwise, 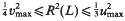 . This is a refinement of a result of Norton ([3], Ch. 22).
. This is a refinement of a result of Norton ([3], Ch. 22).