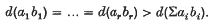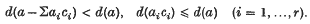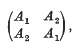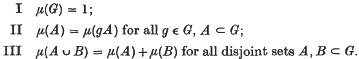Research Article
Two classical lattice point problems
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 699-721
-
- Article
- Export citation
Testing the independence of a system of axioms, using a logical computer
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 443-448
-
- Article
- Export citation
On Chern Characters and the Structure of the unitary group
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 189-199
-
- Article
- Export citation
Degree Functions in Local Rings
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 1-7
-
- Article
- Export citation
Waring's problem in algebraic number fields
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 449-459
-
- Article
- Export citation
Bordism and Cobordism
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 200-208
-
- Article
- Export citation
A geometrical model for the real number field
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 722-727
-
- Article
- Export citation
a-Transforms of Local Rings and a Theorem on Multiplicities of Ideals
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 8-17
-
- Article
- Export citation
Tensor operators under semi-simple groups
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 460-468
-
- Article
- Export citation
The determination of the class-numbers of totally real cubic fields
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 728-730
-
- Article
- Export citation
On the Hausdorff measure of Brownian paths in the plane
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 209-222
-
- Article
- Export citation
On a Generalization of the Euclidean Algorithm
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 18-30
-
- Article
- Export citation
Representations of the n-dimensional rotation group
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 469-475
-
- Article
- Export citation
A finiteness theorem in homological algebra
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 31-36
-
- Article
- Export citation
Bott Periodicity and the Parallelizability of the spheres
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 223-226
-
- Article
- Export citation
On the cohomology of certain groups
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 731-733
-
- Article
- Export citation
Eigenvalues of Composite Matrices
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 37-49
-
- Article
- Export citation
On homotopy Abelian H-spaces
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 734-745
-
- Article
- Export citation
On a class of non-measurable groups
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 227-229
-
- Article
- Export citation
Construction of orders in Abelian groups
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 476-482
-
- Article
- Export citation

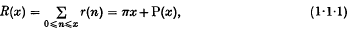

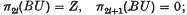
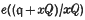 of the ideal
of the ideal 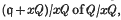 , where
, where 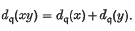
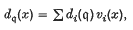
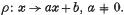 It is the purpose of the present note to show that the system of axioms in (3) (cf. (L. 1)–(L. 5) of this note) leads in a natural way to a model of the real number field. Our method is suggested by a result of Hall ((4), p. 382), namely, that an infinite doubly transitive Frobenius group is isomorphic to the group of affine transformations in a near-field, provided that there is at most one transformation displacing all points and taking a given point
It is the purpose of the present note to show that the system of axioms in (3) (cf. (L. 1)–(L. 5) of this note) leads in a natural way to a model of the real number field. Our method is suggested by a result of Hall ((4), p. 382), namely, that an infinite doubly transitive Frobenius group is isomorphic to the group of affine transformations in a near-field, provided that there is at most one transformation displacing all points and taking a given point 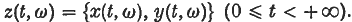 . we assume that there is a probability measure μ defined on a Borel field
. we assume that there is a probability measure μ defined on a Borel field 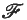 of (measurable) subsets of Ω, so that the system (Ω,
of (measurable) subsets of Ω, so that the system (Ω, 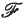 , μ) forms a mathematical model for Brownian paths in the plane. [For details of the definition of μ, see for example (9).]
, μ) forms a mathematical model for Brownian paths in the plane. [For details of the definition of μ, see for example (9).]