Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-30T20:19:50.571Z Has data issue: false hasContentIssue false
  • English
  • Français

Degree Functions in Local Rings

Published online by Cambridge University Press:  24 October 2008

D. Rees
D. Rees
Affiliation:
Department of MathematicsUniversity of Exeter
Get access Rights & Permissions [Opens in a new window]

Extract

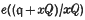Let Q be a local domain of dimension d with maximal ideal m and let q be an m-primary ideal. Then we define the degree function dq(x) to be the multiplicity of the ideal 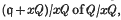, where x; is a non-zero element of m. The degree function was introduced by Samuel (5) in the case where q = m. The function dq(x) satisfies the simple identity

The main purpose of this paper is to obtain a formula

where vi(x) denotes a discrete valuation centred on m (i.e. vi(x) ≥ 0 if x ∈ Q, vi(x) > 0 if x ∈ m) of the field of fractions K of Q. The valuations vi(x) are assumed to have the further property that their residue fields Ki have transcendence degree d − 1 over k = Q/m. The symbol di(q) denotes a non-negative integer associated with vi(x) and q which for fixed q is zero for all save a finite set of valuations vi(x).

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 57 , Issue 1 , January 1961 , pp. 1 - 7
Copyright
Copyright © Cambridge Philosophical Society 1961

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Nagata, M., The theory of multiplicities in general local rings. Proceedings of the International Symposium on Algebraic Number Theory (Tokyo-Nikko, 1955), 191–226.Google Scholar
(2)Northcott, D. G., A general theory of one-dimensional local rings. Proc. Glasgow Math. Ass. 2 (1956), 159–69.CrossRefGoogle Scholar
(3)Rees, D., A note on analytically unramified local rings. J. Lond. Math. Soc. (to appear).Google Scholar
(4)Rees, D., Valuations associated with ideals. Proc. Lond. Math. Soc. (3), 6 (1956), 161–74.CrossRefGoogle Scholar
(5)Samuel, P., Sur les variétés algébroïdes. Ann. Inst. Fourier, 2 (1950), 147–60.CrossRefGoogle Scholar