Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-30T20:03:24.443Z Has data issue: false hasContentIssue false
  • English
  • Français

On a class of non-measurable groups

Published online by Cambridge University Press:  24 October 2008

A. J. Cole  and
S. Świerczkowski
A. J. Cole
Affiliation:
Queen's College, Dundee
S. Świerczkowski
Affiliation:
Institute of Mathematics, Polish Academy of Sciences
Get access Rights & Permissions [Opens in a new window]

Extract

A group G will be called measurable if there exists a real-valued, non-negative set function μ(A) defined on all subsets A ⊂ G which satisfies .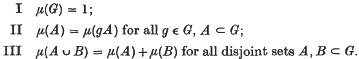

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 57 , Issue 2 , April 1961 , pp. 227 - 229
Copyright
Copyright © Cambridge Philosophical Society 1961

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Kurosh, A. G., The theory of groups (New York, 1956).Google Scholar
(2)Mycielski, J., and Świerczkowski, S., On free groups of motions and decompositions of the Euclidean space. Fund. Math. 45 (1958), 283–91.CrossRefGoogle Scholar
(3)Von Neumann, J., Zur allgemeinen Theorie des Masses. Fund. Math. 13 (1929), 73–116.Google Scholar