Recently Cunningham and Valentine gave in (3) an axiomatic description of the one-dimensional real affine space in terms of its order structure and the (abstract) group of affine transformations 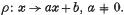It is the purpose of the present note to show that the system of axioms in (3) (cf. (L. 1)–(L. 5) of this note) leads in a natural way to a model of the real number field. Our method is suggested by a result of Hall ((4), p. 382), namely, that an infinite doubly transitive Frobenius group is isomorphic to the group of affine transformations in a near-field, provided that there is at most one transformation displacing all points and taking a given point a into a given point b. The salient point of our investigation is the redundancy of the latter condition in the case where the underlying space is endowed with a certain linear order structure which is invariant under the transformations of the given group.