1. Throughout this note Q will denote a local ring, m will denote its maximal ideal, q will denote a primary ideal belonging to m and k will denote the residue field Q/m. It will not be assumed that k is infinite, but we shall suppose that Q and k both have the same characteristic. Now let υ1, υ2 …,υd be a system of parameters contained in q, so that d = dim Q; then according to the definition given in (2) the ideal (υl υ2,…, υd) is a reduction of q if (υ1 υ2, …, υd) qm = qm+1 for at least one value of m. The use of the concept lies in the fact that such a reduction is, in a certain sense, a very good approximation to q itself; but the notion does, however, suffer from a minor disadvantage in that, if k is finite, q need not have any reductions. In §3 we shall generalize the notion of a reduction in such a way that we overcome this difficulty, and in such a way that the results concerning reductions obtained in (2) acquire some useful extensions.

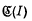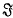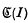
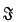
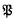
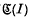
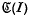
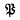
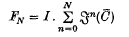
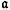Suppose I is a bounded plane continuum whose complement is a single domain (I) and that is a (1–1) bicontinuous transformation of the plane onto itself which leaves I invariant. Cartwright and Littlewood(1) have proved the following theorem:

Theorem A. Suppose that(I) has no prime end fixed underand the frontier of I contains a fixed point P. Ifis any prime end of(I) containing P, and C is any curve in(I) converging tosuch that PeC¯, the closure of C, then for some‡ integer N the continuum I(FN) consisting of

together with the sum B(FN) of its interior complementary domains contains all fixed points in I.

This paper contains a summary of some of the results obtained by the author during a study of the propositional part (denoted by A) of a system of free-from-contradiction, type-free logic set up in 1950 by Ackermann (1). It is shown that in its original form the calculus does not possess the desired properties with respect to equivalence of formulae. A calculus A′, which it is shown may be considered as a ‘minimal’ satisfactory extension of A, is constructed. A′ is compared and contrasted with an alternative form A″ of A given by Ackermann in a paper published in 1952 (2). It is proved that A″ is a proper extension of A′. Among the properties of A′ and A″ which are obtained is the resuit that neither calculus possesses a finite complete model. Reference is made to the solution of the decision problem for A, and it is indicated that it is thought that the corresponding problems can probably be solved for A′ and A″. The proofs of many of the results mentioned in the paper are, if given in detail, rather long. In such cases, from space considerations, only outline proofs are given. Complete proofs are contained in (5), which reference also contains several additional properties of the calculi considered.

This paper contains some contributions to the analytic theory of ideals. The central concept is that of a reduction which is defined as follows: if and 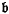are ideals and ⊆ , then is called a reduction of if n = n+1 for all large values of n. The usefulness of the concept depends mainly on two facts. First, it defines a relationship between two ideals which is preserved under homomorphisms and ring extensions; secondly, what we may term the reduction process gets rid of superfluous elements of an ideal without disturbing the algebraic multiplicities associated with it. For example, the process when applied to a primary ideal belonging to the maximal ideal of a local ring gives rise to a system of parameters having the same multiplicity; but the methods work almost equally well for an arbitrary ideal and bring to light some interesting facts which are rather obscured in the special case. The concept seems to be suitable for a variety of applications. The present paper contains one instance which is a generalized form of the associative law for multiplicities (see § 8), and the authors hope to give other illustrations in a separate paper.

The method of leading variables is presented as a new method of solving Linear Programming, and is compared with the Simplex and the Dual Simplex methods.

This note is concerned with pseudo-valuations on a (commutative) field F. A pseudo-valuation on F† is defined as a real-valued function W on F such that

(1) W(x) ≥ 0 for all x∈F and W(0) = 0, but W does not vanish identically on F,

(2) W(xy) ≤ W(x) W(y) for all x, y ∈ F,

(3) W(x−y) ≤ W(x) + W(y) for all x, y ∈ F.

W is non-Archimedean, if it satisfies the ultrametric inequality

(3′) W(x−y) ≤ max {W(x), W(y)}.

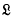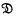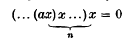
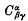1. Let be a Lie ring in which the product of elements x and y is denoted by xy. The inner derivations of , i.e. the mappings X:a→ax for fixed elements x of , form a Lie ring under the product [X, Y] = XY – YX, and the mapping x→ X is a homo-morphism of onto . We shall say that satisfies the nth Engel condition if Xn = 0 for all X in , i.e. if

for all a, x; in . If satisfies the maximum condition on subrings, it is known (1) that this condition implies the nilpotence of ; indeed, must then be nilpotent even if the integer n is allowed to depend on the element X of . We consider here the case in which n is independent of X but does not necessarily satisfy the maximum condition, and inquire whether is then nilpotent.

It is a familiar fact that the Picard surface (or hyperelliptic surface of rank 1) admits a completely transitive permutable continuous group of ∞2 automorphisms. There are, however, other non-scrollar surfaces which possess continuous groups of automorphisms, namely, the elhptic surfaces. Every elliptic surface V2 contains a pencil of birationally equivalent elhptic curves, which are the trajectories of the group in question; it also contains a second, elliptic, pencil of birationally equivalent curves; the intersection number of the two pencils is an important character, known as the determinant of V2. Just as any Picard surface can be mapped on a multiple Picard surface of divisor unity, so V2 can be mapped on a multiple elliptic surface of determinant unity, the branch curve (if any) corresponding to a certain number of trajectories.

Introduction. The present paper is concerned with the conformal geometry of Hermitian spaces. In the first part we find a necessary and sufficient condition for a Hermitian space to be conformally Kähler, that is, conformal to some Kähler space. The condition is that a certain conformal tensor, , vanishes identically. Then, defining a Hermitian manifold as in Hodge (3), we consider such a manifold where the restriction is made that at every point the tensor is zero. This will be called a conformally Kähler manifold, and conditions under which it may be given a Kähler metric are obtained. It is found that any conformally Kähler manifold may be given a Kähler metric provided it is simply-connected or that its fundamental group is of finite order.

In (1), Higman introduces the unrestricted free product of a set of groups, and gives it a natural topology. When this set is an infinite sequence of free cyclic groups he denotes by F their unrestricted free product; we shall denote by K the product for a general sequence {Gn} and, throughout the paper, we assume that each Gn is non-trivial and countable. Higman proves as an incidental result that the commutator subgroup [F, F] is not closed in the topological group F, and the first object of this note is to generalize this result to K. From this, the more interesting deduction immediately follows that K is never equal to L = [K, K]. Indeed, we prove in fact that the cardinal of L and its index in K are both c, the cardinal of the continuum.

1. Statement of problem and the method of Barnes and Swinnnerton-Dyer. 1·1. Let ξ1, ξ2, … ξn De n real, homogeneous linear forms in the real variables x1, x2,…, xn and of determinant Δ ǂ 0. Let y1y2, …, yn be any real numbers. We identify the n-tuplet (x1x2, …, xn) with the point P, coordinates (x1, x2, …, xn), of n-dimensional space.We write P≡P0 (mod 1) if x1≡y1, x2≡y2, …, xn≡yn (mod 1), and P0 is the point (y1, …, yn).

This note describes a simple method of solving the matrix forms of the customary families of finite difference equations which approximate to Poisson's equation (in three dimensions as well as two) and to the bi-harmonic equation. It is intended for use where the boundary of the region over which a solution is wanted is comparatively simple, that is to say, can be subdivided into a comparatively few rectangular areas or rectangular parallelepipeds.

The problem of finding the latent roots and vectors of matrices has been treated in a number of papers ((2)–(7)) mainly from the point of view of desk computers. In this paper the problem is treated from the standpoint of users of high-speed automatic computers. In the first section a number of iterative processes are described and, in the second, the techniques developed for using these processes on the Pilot Model of the Automatic Computing Engine. It is shown that the methods give very high accuracy and can be used to deal with matrices of high orders even on a machine of very limited storage capacity. They have been used on numerous matrices of orders up to 60 mainly on problems arising in the aircraft industry and on eigenvalue problems for systems of ordinary differential equations.

The triple Whitehead product we consider in this note is [[ɩn, ɩn], ɩn] ∈ π3n−2(Sn), where ɩn generates πn(Sn). It follows from the Jacobi identity for Whitehead products

α ∈ πp(X), β ∈ πq(X), γ ∈ πr(X), that 3[[ɩn, ɩn], ɩn] = 0. Now, if n is odd, 2[ɩn, ɩn] = 0, so that 2[[ɩn, ɩn], ɩn] = 0, whence

1. Mahler (1) has obtained a number of valuable existence theorems for homogeneous problems in the geometry of numbers. It appears that no analogous results for inhomogeneous problems have yet been published; and although none of them present great difficulty, it is convenient for applications to have them in print.

In this paper we determine the first minimum of a class of linear forms associated with certain cubic fields that depend on a parameter.

1·1. The differential equation (E) of the title, which occurred in connexion with a problem of electrical engineering, was mentioned to the author by Miss M. L. Cart-wright. It is of some general interest in that, as will be shown, it may have a non-trivial periodic solution (p.s.), although the damping changes sign only once.

The calculation of the diffraction pattern for an out-of-focus line source viewed through an axially symmetrical lens involves the evaluation of the integral

for a constant value of β (related to the numerical aperture of the lens) and a range of values of x and y. For small values of x and y this can best be done by quadrature; for larger values of x or y or both it is more practicable to use numerical evaluation of an appropriate ordinary differential equation. It is shown that the variation of

with x for y = 0, and with y for x = const., can both be expressed by second-order ordinary differential equations of a convenient form for numerical integration; the evaluation of I1(x, y) from solutions of these equations is straightforward. For comparison with experiment, results are required in the form of I1(x, y) and a derived quantity as functions of y, at relatively widely spaced values of x; numerical work for β = 0.72 has been carried out on the EDSAC and has been organized to produce the results in the required form directly, without interpolation.

Comparison of results obtained by using different Gauss quadrature formulae and different interval lengths show some interesting features of the errors of high-order integration formulae, and show that care is necessary in estimating these errors from the differences between quadratures carried out with intervals of different lengths.

It has been known for some time that there are sets in Euclidean space which are of infinite measure in a certain Hausdorff dimension, say α, and yet which contain no subsets that are of finite positive a measure. The properties of such a set, say X, could be developed in much the same way as those of sets which are of positive finite α measure, if there existed a Caratheodory outer measure Γ, defined over the subsets of X, which was such that ∞ > Γ(X) > 0, and for any subset Y of X, Λα (Y) = 0 implied Γ (Y) = O. The object of this note is to show that there are sets for which no such outer measure exists. It is shown that a set defined by Sierpinski (7) is one-dimensional and is such that any Caratheodory outer measure defined over its subsets either takes infinite values or is identically zero or is not zero for all subsets that consist of a single point. It has been remarked by Prof. Besicovitch that these properties imply that the set is measurable with respect to any Caratheodory outer measure defined over subsets of the plane, and in fact any subset is measurable with respect to any such outer measure.

Given a plane set E, we denote by Ex the set of its points whose abscissae are equal to x.

Throughout this paper we use the letters A and B to denote subsets of the x-axis and y-axis respectively, and we denote by A × B their Cartesian product set. We use the letters s and t to denote positive numbers; we denote by ΛsE the outer Hausdorff s-dimensional measure of the set E.