Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-28T13:53:58.113Z Has data issue: false hasContentIssue false
  • English
  • Français

Fixed points on rotating continua

Published online by Cambridge University Press:  24 October 2008

E. R. Reifenberg
E. R. Reifenberg
Affiliation:
Trinity CollegeCambridge
Get access Rights & Permissions [Opens in a new window]

Extract

Suppose I is a bounded plane continuum whose complement is a single domain 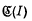(I) and that 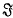is a (1–1) bicontinuous transformation of the plane onto itself which leaves I invariant. Cartwright and Littlewood(1) have proved the following theorem:

Theorem A. Suppose that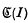(I) has no prime end fixed under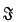and the frontier of I contains a fixed point P. If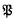is any prime end of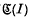(I) containing P, and C is any curve in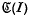(I) converging to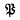such that PeC¯, the closure of C, then for some‡ integer N the continuum I(FN) consisting of

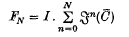
together with the sum B(FN) of its interior complementary domains contains all fixed points in I.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 50 , Issue 1 , January 1954 , pp. 1 - 7
Copyright
Copyright © Cambridge Philosophical Society 1954

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Cartwright, M. L. and Littlewood, J. E.Some fixed point theorems. Ann. Math., Princeton, (2), 54 (1951), 1–37.CrossRefGoogle Scholar
(2)Newman, M. A.Topology of plane sets (Cambridge, 1939).Google Scholar
(3)Reifenberg, E. R.A separationtheorem for finite sets of plane continua. Proc. Camb. phil. Soc. 49 (1953), 573.CrossRefGoogle Scholar