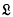1. Let be a Lie ring in which the product of elements x and y is denoted by xy. The inner derivations of 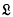, i.e. the mappings X:a→ax for fixed elements x of 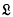, form a Lie ring 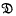under the product [X, Y] = XY – YX, and the mapping x→ X is a homo-morphism of 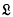onto 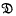. We shall say that 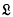satisfies the nth Engel condition if Xn = 0 for all X in 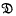, i.e. if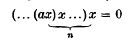

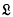for all a, x; in . If 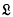satisfies the maximum condition on subrings, it is known (1) that this condition implies the nilpotence of 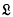; indeed, 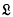must then be nilpotent even if the integer n is allowed to depend on the element X of 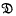. We consider here the case in which n is independent of X but 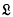does not necessarily satisfy the maximum condition, and inquire whether 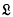is then nilpotent.