Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-30T20:22:13.837Z Has data issue: false hasContentIssue false
  • English
  • Français

The evaluation of a diffraction integral

Published online by Cambridge University Press:  24 October 2008

D. R. Hartree
D. R. Hartree
Affiliation:
Cavendish LaboratoryCambridge
Get access Rights & Permissions [Opens in a new window]

Extract

The calculation of the diffraction pattern for an out-of-focus line source viewed through an axially symmetrical lens involves the evaluation of the integral

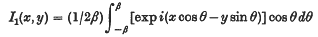
for a constant value of β (related to the numerical aperture of the lens) and a range of values of x and y. For small values of x and y this can best be done by quadrature; for larger values of x or y or both it is more practicable to use numerical evaluation of an appropriate ordinary differential equation. It is shown that the variation of

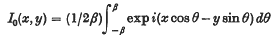
with x for y = 0, and with y for x = const., can both be expressed by second-order ordinary differential equations of a convenient form for numerical integration; the evaluation of I1(x, y) from solutions of these equations is straightforward. For comparison with experiment, results are required in the form of I1(x, y) and a derived quantity as functions of y, at relatively widely spaced values of x; numerical work for β = 0.72 has been carried out on the EDSAC and has been organized to produce the results in the required form directly, without interpolation.

Comparison of results obtained by using different Gauss quadrature formulae and different interval lengths show some interesting features of the errors of high-order integration formulae, and show that care is necessary in estimating these errors from the differences between quadratures carried out with intervals of different lengths.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 50 , Issue 4 , October 1954 , pp. 567 - 574
Copyright
Copyright © Cambridge Philosophical Society 1954

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Gandy, R. O.Proc. phys. Soc., Lond. (in the Press).Google Scholar
(2)Gill, S.Proc. Camb. phil. Soc. 47 (1951), 96.Google Scholar
(3)Milne-Thomson, L. M.The calculus of finite differences (London, 1933), §7·31.Google Scholar
(4)Mitchison, J. M.J. exp. Biol. 30 (1953), 397 (see particularly p. 423 (Appendix 1, §C)).Google Scholar
(5)Richardson, E. G.Phil. Trans. A, 226 (1927), 300.Google Scholar
(6)Wilkes, M. V., Wheeler, D. J. and Gill, S.Preparation of programs for an electronic digital computer (Cambridge, Mass., 1951).Google Scholar