Research Article
Groups with many characteristically simple subgroups: To Philip Hall on his 75th Birthday
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 193-198
-
- Article
- Export citation
On centralizers of involutions in 2-groups
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 199-204
-
- Article
- Export citation
Subrings of the first neighbourhood ring
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 205-214
-
- Article
- Export citation
On fibre spaces and nilpotency. II
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 215-218
-
- Article
- Export citation
On the nth root set of an element in a connected semisimple Lie group
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 219-226
-
- Article
- Export citation
Splitting of some more spaces
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 227-236
-
- Article
- Export citation
The Adams–Mahowald conjecture on real projective spaces
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 237-242
-
- Article
- Export citation
Not all H′-algebras are operator algebras
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 243-250
-
- Article
- Export citation
On the Dixmier property of certain algebras
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 251-260
-
- Article
- Export citation
Equivalent norms on Banach Jordan algebras
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 261-270
-
- Article
- Export citation
Spectra of approximate identities in Banach algebras
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 271-278
-
- Article
- Export citation
Strong and absolute summabilities of functions based on (D, α) summability methods
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 279-286
-
- Article
- Export citation
Abelian theorems for the distributional Stieltjes transformation
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 287-294
-
- Article
- Export citation
Convex fundamental regions for Fuchsian groups: II
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 295-300
-
- Article
- Export citation
Subsequence principles for vector-valued random variables
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 301-312
-
- Article
- Export citation
Multi-indexing and multiple clustering
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 313-338
-
- Article
- Export citation
Total positivity and the embedding problem for Markov chains
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 339-344
-
- Article
- Export citation
Random evolutions and the spectral radius of a non-negative matrix
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 345-350
-
- Article
- Export citation
Contractive inhomogeneous products of non-negative matrices
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 351-364
-
- Article
- Export citation
Cut points, conjugate points and Lorentzian comparison theorems
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 365-384
-
- Article
- Export citation

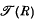 of ideals
of ideals 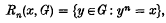
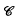 and a ‘Π-space’
and a ‘Π-space’ 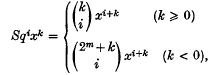
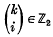 are binomial coefficients modulo 2 and
are binomial coefficients modulo 2 and 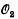 (5) has the Dixmier property. As a corollary of the proof we obtain that the relative commutant of the Choi algebra (4) in
(5) has the Dixmier property. As a corollary of the proof we obtain that the relative commutant of the Choi algebra (4) in 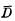 (the closure of
(the closure of 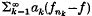 converges almost surely whenever
converges almost surely whenever 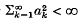 . Komlós(5) has shown that if (
. Komlós(5) has shown that if (