No CrossRef data available.
Convex fundamental regions for Fuchsian groups: II
Published online by Cambridge University Press: 24 October 2008
Extract
1. Introduction. In this article we continue the work begun in (5). We will consider only finitely generated Fuchsian groups of the first kind. Let G be such a group acting on the unit disc Δ. A fundamental domain D for G is a connected open set with the property that any point of Δ is G-equivalent to exactly one point in D or at least one point in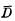 
(the closure of D in Δ). A fundamental domain is said to be locally finite if there are no points in Δ where infinitely many G-images of D accumulate.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 86 , Issue 2 , September 1979 , pp. 295 - 300
- Copyright
- Copyright © Cambridge Philosophical Society 1979
References
REFERENCES
(1)Beardon, A. F. Fundamental domains for Kleinian groups. In Discontinuous groups and Riemann surfaces. Annals of Math. Studies no. 79, pp. 31–41 (Princeton University Press, 1974).CrossRefGoogle Scholar
(2)Beardon, A. F. and Maskit, B.Limit points of Kleinian groups and finite sided fundamental polyhedra. Acta Math. 132 (1974), 1–12.CrossRefGoogle Scholar
(3)Greenberg, L. Finiteness theorems for Fuchsian and Kleinian groups. Discrete groups and Automorphic Functions, ed. Harvey, W. J. (London, Academic Press, 1977).Google Scholar
(4)Keen, L.Canonical polygons for finitely generated Fuchsian groups. Acta Math. 115 (1966), 1–16.CrossRefGoogle Scholar
(5)Nicholls, P. and Zarrow, R.Convex fundamental regions for Fuchsian groups. Math. Proc. Cambridge Philos. Soc. 84 (1978), 507–518.CrossRefGoogle Scholar
(6)Purzitsky, N.Canonical generators of Fuchsian groups. Illinois J. Math. 18 (1974), 484–490.CrossRefGoogle Scholar
(7)Zieschang, H.Algorithmen für einfache kurven auf Flächen. Math. Scand. 17 (1965), 17–40.CrossRefGoogle Scholar