Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-28T13:20:59.384Z Has data issue: false hasContentIssue false
  • English
  • Français

The Adams–Mahowald conjecture on real projective spaces

Published online by Cambridge University Press:  24 October 2008

Wen-Hsiung Lin
Wen-Hsiung Lin
Affiliation:
National Cheng-Chi University, Taipei, Taiwan, Republic of China
Get access Rights & Permissions [Opens in a new window]

Extract

Let A denote the mod 2 Steenrod algebra. Let ℤ2[x, x−l] be the (graded) ring of finite Laurent series over ℤ2 in the variable x with dim (x) = 1. ℤ2[x, x−1] is a module over the Steenrod algebra A by

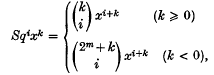
where 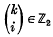are binomial coefficients modulo 2 and m > 0 is large compared with |k| and i. Let M be the A-submodule of ℤ2[x, x−1 ] generated by all powers xi with i ≠ −1. It is easy to see that ℤ2 [,x, x−1]/M ≅ σ−1ℤ2 (means ℤ2 on dimension − 1). Let ρ: ℤ2[x, x−1] → σ−1 ℤ2 be the projection map.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 86 , Issue 2 , September 1979 , pp. 237 - 242
Copyright
Copyright © Cambridge Philosophical Society 1979

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Adams, J. F.Vector fields on spheres. Ann. of Math. 75 (1962), 603–632.CrossRefGoogle Scholar
(2)Adams, J. F.Operations of the n-th kind in K-theory and what we don't know about ℝP ∞. London Math. Soc. Lect. Note Series, no. 11 (Cambridge University Press, 1974).Google Scholar
(3)Atiyah, M. F.Thom complexes, Proc. London Math. Soc. (3) 11, (1961), 291–310.CrossRefGoogle Scholar
(4)May, J. P.The cohomology of restricted Lie algebras and Hopf algebras. J. of Algebra 3 (1966), 123–146.CrossRefGoogle Scholar
(5)Milnor, J. W.The Steenrod algebra and its dual. Ann. of Math. 67 (1958), 150–171.CrossRefGoogle Scholar