1. Simple linear clustering. One of the simplest clustering problems is the following: if n points are taken independently and uniformly at random on the interval I = [0, L], what is the probability Q = Q(n, a, L) that no two points are closer than a? The well-known answer

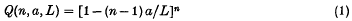
if (n − 1) a ≤ L, and Q = 0 otherwise, can be obtained in a variety of ways. Perhaps the simplest one is the original method of E.C.Molina(5). If x1,…,xn are the abscissas of the n points, then there are n! equiprobable orderings of the xi's consistent with the condition that no two points are closer than a. The probability of each one is

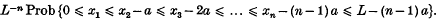
Let yi = xi − (i − 1) a for i = 1,…,n, then the above becomes

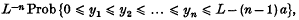
which is