The packing problem for (k, 3)-caps is that of finding (m, 3)r, q, the largest size of (k, 3)-cap in the Galois space Sr, q. The problem is tackled by exploiting the interplay of finite geometries with error-correcting codes. An improved general upper bound on (m, 3)3 q and the actual value of (m, 3)3, 4 are obtained. In terms of coding theory, the methods make a useful contribution to the difficult task of establishing the existence or non-existence of linear codes with certain weight distributions.

It has been known for some time ((6), p. 270; (4), theorem 9·19) that if is a Boolean topos, then the full subcategory Kf of Kuratowski-finite objects in is again a topos. For a non-Boolean topos , however, Kf need not be a topos, as can be seen when is the Sierpinski topos ((1), example 7·1); on the other hand, two other full subcategories of , coinciding with Kf when is Boolean, suggest themselves as candidates for a subtopos of finite objects. Of one of these, the category dKf of decidable K-finite objects in , the Main Theorem of (1) asserts that it is always a (Boolean) topos. The other is the category sKf of -subobjects of K-finite objects. The inclusions

dKf ⊆ Kf ⊆ sKf are clear.

are clear.

Selmer(1) conjectured that the Hasse principle holds for all cubic surfaces of the type

that is, such a surface has a rational point whenever it has points defined over every p-adic field Qp; and he proved this assertion in the case that ab = cd.

The work of this note was motivated in the first place by North-cott's theory of dilatations for one-dimensional local rings (see, for example (4) and (5)). This produces a tree of local rings as in (4) which corresponds, in the abstract case, to the branching sequence of infinitely-near multiple points on an algebroid curve. From the algebraic point of view it seems more natural to characterize such one-dimensional local rings R by means of the set of rings which arise by blowing up all ideals Q which are primary for the maximal ideals M of R. This set of rings forms a lattice (R), ordered by inclusion, each ring S of which is a finite R-module. Moreover the length of the R-module S/R is just the reduction number of the corresponding ideal Q (cf. theorem 1 of Northcott (6)). Thus the lattice (R) provides a finer classification of the rings R than does the set of reduction numbers (cf. Kirby (1)).

Following P. F. Pickel (5) we write (G) for the set of isomorphism classes of finite quotients of a group G. One of the outstanding problems in the theory of polycyclic groups is to determine whether there can be infinitely many non-isomorphic polycyclic groups G with a given (G). We solve a special case of this problem with our first main result:

Theorem 1. Let G be an abelian-by-cyclic polycyclic group. Then the polycyclic-by-finite groups H withlie in only finitely many isomorphism classes.

Two recent results relate the existence of injective modules for group algebras which are ‘small’ in some sense to the structure of the group.

(1) The trivial kG-module is injective if and only if G is a locally finite group with no elements of order p = char k (9).

(2) If (G) is a countable group, then every irreducible kG-module is injective if and only if G is a locally finite p′ group which is abelian-by-finite (9) and (11)

In the present article we prove a result characterizing the Jordan analogues of B*-algebras among the complex Banach Jordan algebras in terms of the algebra and norm structures alone.

Let A be a C*-algebra with centre Z. If a ∈ A, the bounded linear mapping x → + ax – xa (x ∈ A) is called the inner derivation of A induced by a, and we denote it by D(a, A). A simple application of the triangle inequality shows that

where d (a; Z) denotes the distance from a to Z in the normed space A.

Given Banach spaces X and Y let (X, Y) be the space of germs at 0 of C∞ Y-valued mappings defined on neighbourhoods of 0 in X. Let j(X, Y) be those f ∈ (X, Y) such that the ith derivative f(i)(0) = 0 for i = 0,1,…, j – 1. Abbreviations: (X) for (X, ℝ) and j(X) for j(X, ℝ). For ease of exposition germs will often be replaced by mappings which ‘represent’ them.

1. The set ℰ (X) of homotopy classes of self-homotopy equivalences of a space X forms a group under composition. In this note I complete the calculation of ℰ (X) when X is a torsion free rank 2 h-space, and give ℰ (X) up to extension for the remaining principal S3 bundles over S7.

In this final sequel to (9), I shall prove a general consistency statement which seems to me to complete the foundations of infinite loop space theory. In particular, this result will specialize to yield the last step of the proof of the following theorem about the stable classifying spaces of geometric topology.

Let S be a (jointly continuous) topological semigroup, C(S) the set of all bounded complex-valued continuous functions on S and M (S) the set of all bounded complex-valued Radon measures on S. Let (S) (or (S)) be the set of all µ ∈ M (S) such that x → │µ│ (x-1C) (or x → │µ│(Cx-1), respectively) is a continuous mapping of S into ℝ, for every compact set C ⊆ S, and . (Here │µ│ denotes the measure arising from the total variation of µ and the sets x-1C and Cx-1 are as defined in Section 2.) When S is locally compact the set Ma(S) was studied by A. C. and J. W. Baker in (1) and (2), by Sleijpen in (14), (15) and (16) and by us in (3). In this paper we show that some of the results of (1), (2), (14) and (15) remain valid for certain non-locally compact S and raise some new problems for such S.

This note is a sequel to the paper referred to in the title, (2). Its purpose is to sharpen theorem 1 of that paper. We first set up some notation.

1. Consider the constant-coefficient fifth-order differential equation:

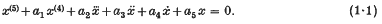
It is known from the general theory that the trivial solution of (1·1) is unstable if, and only if, the associated (auxiliary) equation:

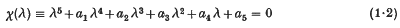
has at least one root with a positive real part. The existence of such a root naturally depends on (though not always all of) the coefficients a1, a2,…, a5. For example, if

it is clear from a consideration of the fact that the sum of the roots of (1·2) equals ( – a1) that at least one root of (1·2) has a positive real part for arbitrary values of a2,…, a5. A similar consideration, combined with the fact that the product of the roots of (1·2) equals ( – a5) will show that at least one root of (1·2) has a positive real part if

for arbitrary a2, a3 and a4. The condition a1 = 0 here in (1·4) is however superfluous when

for then X(0) = a5 < 0 and X(R) > 0 if R > 0 is sufficiently large thus showing that there is a positive real root of (1·2) subject to (1·5) and for arbitrary a1, a2, a3 and a4.

Let {Xn} be a sequence of iid random variables. If the common charac-teristic function is absolutely integrable in mth power for some integer m ≥ 1, then Zn = n−½(X1 + … + Xn) has a pdf fn for all n ≥ m. Here we give a necessary and sufficient condition for sup asn. → ∞, where φ (x) is the standard normal pdf and M(x) is a non-decreasing function of x ≥ 0 such that M(0) > 0 and M(x)/xδ is non-increasing for 0 < δ ≤ 1.

It is often of greater practical value to have results about queueing theory which involve probabilities rather than characteristic functions. To quote Kendall (4), section 5, ‘These results of Prabhu, further exploited by himself and Takács, are rapidly raising the Laplacian curtain which has hitherto obscured much of the details of the queue-theoretic scene’. In this paper we derive the exponential limit formula for the equilibrium waiting time distribution function G, for the queue GI/G/1 in heavy traffic, using stochastic bounds which are asymptotically sharp as the traffic intensity (defined below) increases to unity (which has not been done before to the author's knowledge). This formula was derived by Kingman (5), (6) and (9), using characteristic functions, who, in section 9 of the latter paper, stressed the need for improving the precision of the approximation ‘by giving inequalities, bounds for errors, and generally by setting the theory on a more elegant and rigorous basis’. Kingman (6) and (9) also sketched a proof of the same result using a Brownian approximation, which was done in detail by Viskov (18); but here again the same difficulties are present in practical interpretation, error bounds etc.