Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-28T14:03:22.292Z Has data issue: false hasContentIssue false
  • English
  • Français

Determinacy in a class of germs on a reflexive Banach space

Published online by Cambridge University Press:  24 October 2008

R. J. Magnus
R. J. Magnus
Affiliation:
University of Iceland, Dunhaga 3, Reykjavik
Get access Rights & Permissions [Opens in a new window]

Extract

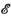Given Banach spaces X and Y let (X, Y) be the space of germs at 0 of C∞ Y-valued mappings defined on neighbourhoods of 0 in X. Let 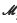j(X, Y) be those f ∈ 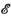(X, Y) such that the ith derivative f(i)(0) = 0 for i = 0,1,…, j – 1. Abbreviations: 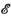(X) for 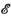(X, ℝ) and 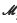j(X) for 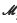j(X, ℝ). For ease of exposition germs will often be replaced by mappings which ‘represent’ them.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 84 , Issue 2 , September 1978 , pp. 293 - 302
Copyright
Copyright © Cambridge Philosophical Society 1978

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Zeeman, E. C. and Trotman, D. J. A.The classification of elementary catastrophes of codimension ≤ 5. Symposium on catastrophe theory, Seattle, 1975 (Berlin, Springer–Verlag, 1976).Google Scholar
(2)Bröcker, Th.Differentiable germs and catastrophes (Cambridge: Cambridge University Press, 1975).CrossRefGoogle Scholar
(3)Palais, R. S.The Morse lemma for Banach spacca. Bull. Amer. Math. Soc. 75 (1969), 968–971.CrossRefGoogle Scholar
(4)Mather, J. N.Stability of C∞ mappings. V. Transversality. Advances in Math. 4 (1970), 301–336.CrossRefGoogle Scholar
(5)Thom, R.Stabilité structurelle et morphogénèse (New York: Benjamin, 1972).Google Scholar
(6)Gromoll, D. and Meyer, W.On differentiable functions with isolated critical points. Topology 8 (1969), 361–369.CrossRefGoogle Scholar
(7)Abraham, R. and Robbin, J.Transversal mappings and flows (New York: Benjamin, 1967).Google Scholar
(8)Magnus, R. J.On the orbits of a Lie group action. Battelle–Geneva math. report no. 105.Google Scholar
(9)Magnus, R. J.On universal unfoldings of certain real functions on a Banach space. Math. Proc. Cambridge Philos. Soc. 81 (1977), 91–95.CrossRefGoogle Scholar
(10)Rand, D.Arnold's classification of simple singularities of smooth functions. Preprint of the Mathematics Institute, University of Warwick, April 1977.Google Scholar