Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-28T13:25:19.099Z Has data issue: false hasContentIssue false
  • English
  • Français

Algebras of measures on C-distinguished topological semigroups

Published online by Cambridge University Press:  24 October 2008

H. A. M. Dzinotyiweyi
H. A. M. Dzinotyiweyi
Affiliation:
Katholieke Universiteit, Nijmegen, Netherlands
Get access Rights & Permissions [Opens in a new window]

Extract

Let S be a (jointly continuous) topological semigroup, C(S) the set of all bounded complex-valued continuous functions on S and M (S) the set of all bounded complex-valued Radon measures on S. Let 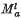(S) (or 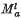(S)) be the set of all µ ∈ M (S) such that x → │µ│ (x-1C) (or x → │µ│(Cx-1), respectively) is a continuous mapping of S into ℝ, for every compact set C ⊆ S, and 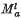. (Here │µ│ denotes the measure arising from the total variation of µ and the sets x-1C and Cx-1 are as defined in Section 2.) When S is locally compact the set Ma(S) was studied by A. C. and J. W. Baker in (1) and (2), by Sleijpen in (14), (15) and (16) and by us in (3). In this paper we show that some of the results of (1), (2), (14) and (15) remain valid for certain non-locally compact S and raise some new problems for such S.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 84 , Issue 2 , September 1978 , pp. 323 - 336
Copyright
Copyright © Cambridge Philosophical Society 1978

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Baker, A. C. and J. W., Algebras of measures on a locally compact semigroup: II. J. London Math. Soc. 2 (1970), 651–659.CrossRefGoogle Scholar
(2)Baker, A. C. and J. W., Algebras of measures on a locally compact semigroup: III. J. London Math. Soc. 4 (1972), 685–695.CrossRefGoogle Scholar
(3)Dzinotyiweyi, H. A. M.Locally quasi-invariant measures. J. London Math. Soc. 15 (1977), 484–488.CrossRefGoogle Scholar
(4)Giles, R.A generalization of the strict topology. Trans. Amer. Math. Soc. 161 (1971), 467–474.CrossRefGoogle Scholar
(5)Gowrisankaran, C.Radon measures on groups. Proc. Amer. Math. Soc. 35 (1972), 503–506.CrossRefGoogle Scholar
(6)Grothendieck, A.Sur les applications linéaires faiblement compactes d'espaces du type C(K). Canad. J. Math. 5 (1953), 129–173.CrossRefGoogle Scholar
(7)Hewitt, E. and Ross, K. A.Abstract harmonic analysis, vol. I (Berlin, Springer–Verlag, 1963).Google Scholar
(8)Hirschfeld, R.On measures in completely regular spaces. Bull. Belg. Math. Soc. 24 (1972), 274–286.Google Scholar
(9)Hirschfeld, R.RIOTS. Niew Arch. Wisk. 22 (1974), 1–43.Google Scholar
(10)Kelley, J. L.General topology (Princeton, Van Nostrand, 1955).Google Scholar
(11)Paterson, A. L. T.Invariant measure semigroups. Proc. London Math. Soc. 35 (1977), 313–332.CrossRefGoogle Scholar
(12)Schaefer, H. H.Banach lattices and positive operators (Berlin, Heidelberg, New York, Springer–Verlag, 1974).CrossRefGoogle Scholar
(13)Sentilles, F. D.Compactness and convergence in the space of measures. Illinois J. Math. 13 (1969), 761–768.CrossRefGoogle Scholar
(14)Sleijpen, G. L. G. Convolution measure algebras on semigroups. Thesis, Katholieke Universiteit, Toernooiveld, Nijmegen, 1976.Google Scholar
(15)Sleijpen, G. L. G.Locally compact semigroups and continuous translations of measures. Proc. London Math. Soc. (to appear).Google Scholar
(16)Sleijpen, G. L. G.L-multipliers for foundation semigroups with identity element. Report 7716, Math. Instituut, Katholieke Universiteit, Toernooiveld, Nijmegen, 1977.Google Scholar
(17)Taylor, J. L.The structure of convolution measure algebras. Trans. Amer. Math. Soc. 119 (1965), 150–166.CrossRefGoogle Scholar
(18)Yuan, J.On the continuity of convolution. Semigroup Forum 10 (1975), 367–372.CrossRefGoogle Scholar