1. It was shown by Barlotti (1) that the number k of points on a (k, n)-arc of a finite projective piane of order q

and that if q ≢ 0 (mod n) then for n ≥ 3

.

Let φ (X) denote a function satisfying limx→∞, φ(X) = ∞. Let ℬ be a sequence of positive integers and let T(X) = T(X, ℬ, φ) be the set of real numbers y, 1 ≤ y ≤ X, such that the interval (y, y + φ(y)] contains no member of ℬ.

In this paper we consider complex projective surfaces V, defined by an equation of the form fn–1 (x, y, z) w + fn (x, y, z) = 0, where fi is homogeneous of degree i, and relate the geometry of the intersections of the piane projective curves fn–1 = 0 and fn = 0 with the singularities of V. The results we obtain clarify and generalize some of those presented by Bruce and Wall (3).

In this paper we will study the homological properties of the enveloping algebra U = U (Sl2(ℂ)), with particular reference to the homological dimension of simple U-modules and the global dimension of the primitive factor rings of U.

Sandling(6) determined the dimension subgroups of the semidirect product of a normal abelian subgroup and a subgroup; namely if G = NT is the semidirect product of a normal abelian subgroup N and a subgroup T, then the mth dimension subgroup Dm(G) of G is equal to [N, (m – 1) G] · Dm (T) for all m ≧ 1, where

1. Following Lorentz, we suppose throughout that Ω(n) is a non-negati ve non-decreasing function of the non-negative integer n such that Ω(n)→ ∞ as n → ∞. Consider the summability method given by the sequence-to-sequence transformation corresponding to the matrix A = (ank). We say that Ω(n) is a summability function for A (or absolute summability function for A) if the following holds: Any bounded sequence {sn} such that the number of values of ν with ν ≤ n, sν ≠ 0 does not exceed Ω(n) is summable A (or is absolutely summable A, respectively). These definitions are due to Lorentz (4), (6). We shall be concerned with the case in which A is a regular Hausdorff method, say A = H = (H, μn). Then H is given by the matrix (hnk) with

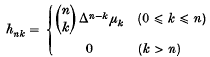
with

X(0) = X(0 + ) = 0, X(1) = 1;(see e.g.(1), chapter XI). We shall suppose throughout that these conditions are satisfied. It is known that H is then necessarily also absolutely regular.

The main properties of the Hausdorff dimension, here denoted by dim, are

In ℝp, in variance under a group Н of homeomorphisms: ∀HεH, dim О H = dim. The definition of H, introduced in (15) and (16), is recalled in § 2.

A unital C*-algebra is said to satisfy the Dixmier property if for each element x in the closed convex hull of all elements of the form u*xu, u being a unitary in , intersects the centre of ((2), 2·7). The von Neumann algebras and also some other classes of C*-algebras are known to satisfy the Dixmier property (cf. (2), (3), (4), (6)). If is a simple C*-algebra which satisfies the Dixmier property then has at most one tracial state. In (3) Archbold raised the question whether there exists a unital simple C*-algebra which has at most one tracial state without satisfying the Dixmier property. In the present note we characterize the unital simple C*-algebras with at most one tracial state in terms of a condition which is similar to the Dixmier property, but is in fact formally weaker in the framework of simple C*-algebras. This characterization relies on the method used by Pedersen in (5) in order to show that for a unital simple C*-algebra which has at most one tracial state and at least one non-trivial projection the linear span of all projections in is dense in As an application we characterize those unital simple C*-algebras with a unique tracial state which satisfy the Dixmier property.

In this paper we extend to certain domains in m-dimensional Euclidean space Rm, m ≥ 3, some results about the boundary behaviour of harmonic functions which, in R2, are known to follow from distortion theorems for conformal mappings.

Let Ll …, Lr be independent linear subspaces of Ed, with di = dim Li ≥ 1 (i = 1, …, r), and Ed = L1 + … + Lr. For each i, let K¯;i be a convex body in Li with 0 ∈ K¯i, Ki = K¯i + ti(ti ∈ Ed) any translate of K¯i, and define K = con v (K1 ∪ … ∪ Kr), and similarl K¯. Then vol K ≥ vol K¯. Necessary and sufficient conditions for equality are also obtained.

Using the decomposition of a certain vector space under the action of the structure group of Riemannian almost product manifolds, A. M. Naveira (9) has found thirty-six distinguished classes of these manifolds. In this article, we prove that this decomposition is irreducible by computing a basis of the space of invariant quadratic forms on such a space.

At the 1977 Georgia Topology Conference, Cappell and Shaneson(6) announced the following theorem.

Let M be a closed oriented smooth four-manifold.

If a second order ordinary differential equation has a simple or a double pole at a point zfl, then the standard Liouville-Green approximation could sometimes be valid near that point. In this paper we present an asymptotic series solution that is always valid near a double pole. A solution for that of a simple pole is also indicated. Asymptotic validity is proved.

A random graph on n vertices is a random subgraph of the complete graph on n vertices. By analogy with this, the present paper studies the asymptotic properties of a random submatroid ωr of the projective geometry PG(r−l, q). The main result concerns Kr, the rank of the largest projective geometry occurring as a submatroid of ωr. We show that with probability one, for sufficiently large r, Kr takes one of at most two values depending on r. This theorem is analogous to a result of Bollobás and Erdös on the clique number of a random graph. However, whereas from the matroid theorem one can essentially determine the critical exponent of ωr, the graph theorem gives only a lower bound on the chromatic number of a random graph.

Recent papers by Atkinson and Reuter(1), Brown and Carr(5), and Barbour(2) have proved several important results concerning wave solutions of the usual deterministic model for the spatial spread of an epidemic, such as measles or influenza. In particular Atkinson and Reuter showed that non-trivial wave solutions, in a population along a line, only exist provided the contact distribution function has an exponentially bounded tail, and that the speed of propagation c must be at least some critical value c0. They constructed a solution for c > c0, which Barbour later showed to be the unique solution, modulo translation, at that speed. Brown and Carr showed that a solution was also possible at speed c0, though it has not been possible to show uniqueness at this speed.