Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-28T13:45:05.714Z Has data issue: false hasContentIssue false
  • English
  • Français

Absolute summability functions for Hausdorff methods

Published online by Cambridge University Press:  24 October 2008

B. Kuttner
B. Kuttner
Affiliation:
University of Birmingham
Get access Rights & Permissions [Opens in a new window]

Extract

1. Following Lorentz, we suppose throughout that Ω(n) is a non-negati ve non-decreasing function of the non-negative integer n such that Ω(n)→ ∞ as n → ∞. Consider the summability method given by the sequence-to-sequence transformation corresponding to the matrix A = (ank). We say that Ω(n) is a summability function for A (or absolute summability function for A) if the following holds: Any bounded sequence {sn} such that the number of values of ν with ν ≤ n, sν ≠ 0 does not exceed Ω(n) is summable A (or is absolutely summable A, respectively). These definitions are due to Lorentz (4), (6). We shall be concerned with the case in which A is a regular Hausdorff method, say A = H = (H, μn). Then H is given by the matrix (hnk) with

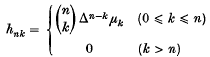
with

X(0) = X(0 + ) = 0, X(1) = 1;(see e.g.(1), chapter XI). We shall suppose throughout that these conditions are satisfied. It is known that H is then necessarily also absolutely regular.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 91 , Issue 1 , January 1982 , pp. 51 - 56
Copyright
Copyright © Cambridge Philosophical Society 1982

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Hardy, G. H.Divergerti series (Oxford, 1949).Google Scholar
(2)Kuttner, B. and Parameswaran, M. R. The converse of a Tauberian theorem for Hausdorff methods. (To appear.)Google Scholar
(3)Kuttner, B. and Parameswaran, M. R. Summability functions for Hausdorff methods. (To appear.)Google Scholar
(4)Lorentz, G. G.A contribution to the theory of divergent series. Acta Math. 80 (1948), 157–190.Google Scholar
(5)Lorentz, G. G.Direct theorems on methods of summability. Canadian J. Math. 1 (1949), 305–319.CrossRefGoogle Scholar
(6)Lorentz, G. G.Direct theorems on methods of summability: II. Canadian J. Math. 3 (1951), 236–256.Google Scholar
(7)Lorentz, G. G. and Macphail, M. S.Direct theorems on methods of summability. III. Absolute summability functions. Math. Zeitschrift 59 (1953), 231–246.CrossRefGoogle Scholar