In a recent paper (3) Diananda has given an extension of the central limit theorem to stationary sequences of random variables {Yt} (t = 1,2,3,…), which are m–dependent, i.e. are such that m + 1 is the smallest integer r having the property that two sets of the Y's are independent whenever the suffix of any member of one set differs from that of any member of the other set by at least r. As Diananda points out, this can be used to show that for linear autoregressive processes with m–dependent residuals, the joint distribution of any finite number of the forms which occur in Bartlett and Diananda's goodness of fit test (see (1)) is asymptotically multivariate normal, provided also that the fourth moment of the residuals is finite. These forms are linear functions of the sample serial correlations rt, and if the autoregressive process is defined by
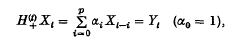
they may be denoted by  , where
, where
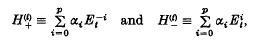
Et being the usual shift operator such that for any function ft defined for integral t, 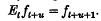 In particular, when
In particular, when 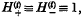 , as for a moving average process, the joint distribution of any finite number of the rt, is asymptotically multivariate normal.
, as for a moving average process, the joint distribution of any finite number of the rt, is asymptotically multivariate normal.