When the boundary-layer approximations are applied to the laminar flow in an axially symmetrical jet of gas with Prandtl number unity, a particular integral of the equations of motion satisfying the required boundary conditions is found to be 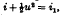, where i1, is the (constant) enthalpy on the jet boundary. By a suitable transformation an equation is obtained which, to a first approximation, may be replaced by the equation for flowin an axially symmetrical jet of incompressible fluid at a sufficiently large distance from the orifice. For an ideal gas, the known solution of this equ`ation may be used as the starting point of an iterative method to build up the stream function as a power series. The next approximation is found explicitly. It shows that for subsonic Mach numbers the density at a point on the axis is greater and the temperature less than on the boundary by amounts which may be very closely represented by terms inversely proportional to the square of the distance of the point from the orifice.