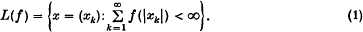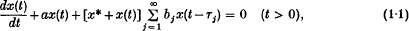Research Article
100 not out
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 1-4
-
- Article
- Export citation
Fourier coefficients of cusp forms
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 5-29
-
- Article
- Export citation
Mordell's finite basis theorem revisited
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 31-41
-
- Article
- Export citation
Boolean algebras in a localic topos
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 43-55
-
- Article
- Export citation
On the analytic equivalence of curves
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 57-64
-
- Article
- Export citation
Vogt's theorem on categories of homotopy coherent diagrams
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 65-90
-
- Article
- Export citation
Generating families for images of Lagrangian submanifolds and open swallowtails
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 91-107
-
- Article
- Export citation
A relationship between link polynomials
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 109-112
-
- Article
- Export citation
A note concerning Seifert manifolds for 2-knots
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 113-116
-
- Article
- Export citation
On even-dimensional fibred knots obtained by plumbing
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 117-131
-
- Article
- Export citation
Additivity and superadditivity in Lp-spaces
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 133-136
-
- Article
- Export citation
Egorov measurability and generator cores
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 137-143
-
- Article
- Export citation
Compact multipliers on weighted hypergroup algebras. II
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 145-149
-
- Article
- Export citation
Some criteria for nuclearity
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 151-159
-
- Article
- Export citation
Sequence spaces defined by a modulus
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 161-166
-
- Article
- Export citation
Some remarks about extreme degrees in a random graph
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 167-174
-
- Article
- Export citation
The reduction of a pair of singular integral equations
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 175-182
-
- Article
- Export citation
On the global attractivity in a generalized delay-logistic differential equation
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 183-192
-
- Article
- Export citation
Front matter
PSP volume 100 issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
PSP volume 100 issue 1 Cover and Back matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b2
-
- Article
-
- You have access
- Export citation

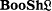 of Boolean algebras in the topos
of Boolean algebras in the topos 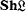 of sheaves on a locale
of sheaves on a locale  and with properties of the initial Boolean algebra in
and with properties of the initial Boolean algebra in