Research Article
A theorem on cardinal numbers associated with a locally compact Abelian group
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 701-704
-
- Article
- Export citation
Inclusion of sets of regular summability matrices
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 705-712
-
- Article
- Export citation
On Künneth suspensions
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 713-720
-
- Article
- Export citation
Complete functors in homology I. Chain maps and endomorphisms
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 721-735
-
- Article
- Export citation
Complete functors in homology II. The exact homology sequence
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 737-749
-
- Article
- Export citation
Chern characters and higher-order cohomology operations
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 751-764
-
- Article
- Export citation
Polynomial modules and general polynomials
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 765-767
-
- Article
- Export citation
A finite set of generators for the homeotopy group of a 2-manifold
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 769-778
-
- Article
- Export citation
Conditions equivalent to central symmetry of convex curves
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 779-785
-
- Article
- Export citation
Covering a sphere with congruent great-circle arcs
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 787-800
-
- Article
- Export citation
The spectra of Fredholm operators in locally convex spaces
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 801-806
-
- Article
- Export citation
Cobordism of combinatorial n – manifolds for n ≤ 8
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 807-811
-
- Article
- Export citation
Locally convex spaces with denumerable systems of weakly compact subsets
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 813-815
-
- Article
- Export citation
Weak Cauchy sequences in normed linear spaces
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 817-819
-
- Article
- Export citation
A counter-example in area theory
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 821-845
-
- Article
- Export citation
On a class of infinite products
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 847-854
-
- Article
- Export citation
On a problem about the Epstein zeta-function
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 855-875
-
- Article
- Export citation
The Tchebysheffian approximation of one rational function by another
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 877-890
-
- Article
- Export citation
Differential inequalities and extension of Lyapunov's method
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 891-895
-
- Article
- Export citation
The numerical solution of the heat conduction equation in one dimension
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 897-907
-
- Article
- Export citation

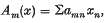
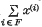 is the null sequence, then
is the null sequence, then 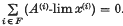 .
.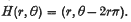
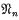 and Ω
and Ω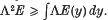 This inequality is known (1,3) when the measures are interpreted aslspherical’. But as has for some time been conjectured and this paper shows, with the proper normalization it is false for the convex case.
This inequality is known (1,3) when the measures are interpreted aslspherical’. But as has for some time been conjectured and this paper shows, with the proper normalization it is false for the convex case.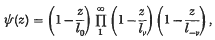
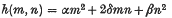
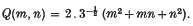
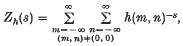
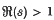 . The function
. The function