Published online by Cambridge University Press: 24 October 2008
In area theory, Hausdorff measure has been mainly used in the form of Hausdorff ‘spherical’ measure (l) in spite of the fact that work on the geometry of sets of points has mainly used Hausdorff ‘convex’ measure (2,4). The reason for this lies in the inequality 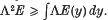 This inequality is known (1,3) when the measures are interpreted aslspherical’. But as has for some time been conjectured and this paper shows, with the proper normalization it is false for the convex case.
This inequality is known (1,3) when the measures are interpreted aslspherical’. But as has for some time been conjectured and this paper shows, with the proper normalization it is false for the convex case.