Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-28T14:09:43.986Z Has data issue: false hasContentIssue false
  • English
  • Français

Inclusion of sets of regular summability matrices

Published online by Cambridge University Press:  24 October 2008

J. W. Baker  and
G. M. Petersen
J. W. Baker
Affiliation:
University College of Swansea
G. M. Petersen
Affiliation:
University College of Swansea
Get access Rights & Permissions [Opens in a new window]

Extract

1. In this paper we wish to discuss some problems which arise from a paper by Lorentz and Zeller; see (5). If {μn} is a fixed sequence monotonically increasing to infinity, and every sequence {sn} summed by both of the regular matrices A = (amn) and B = (bmn) and satisfying sn = O{μn) is summed to the same value by both matrices, the matrices are called (μn)-consistent. The two matrices are called consistent if they are (μn)-consistent for all {μn}, μn↗∞; they are b-consistent if the bounded sequences summed by both are summed to the same value by both. The matrix A is said to be (μn)-stronger than the matrix B, if every sequence {μn} that is B summable and satisfying sn = O(μn) is also A summable. The matrix A is stronger than B if every B summable sequence is A summable; A is b-stronger if every bounded B summable sequence is A summable. The symbol A -lim x denotes the value to which the sequence x = {xn} is summed by A; Am(x) is the transformation

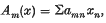
and A(x) is the sequence {Am(x)}. Let {A(i)}i ∈ I be any family, infinite or finite, of regular summability matrices. This family is called simultaneously consistent if, given any finite subset of I, say F, and any set of sequences {x(i)i ∈ F such that A(i) sums x(i) for each i in F, and such that 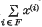is the null sequence, then .

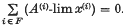Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 60 , Issue 4 , October 1964 , pp. 705 - 712
Copyright
Copyright © Cambridge Philosophical Society 1964

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Banach, S.Théorie des Opérations Linéaires (Warsaw, 1932).Google Scholar
(2)Brudno, A. L.Summation of bounded sequences. Mat. Sb. n.s. 16 (1945), 191–247 (in Russian).Google Scholar
(3)Hardy, G. H.Divergent series (Oxford, 1949).Google Scholar
(4)Henriksen, M.Multiplicative summability methods and the Stone-Čech compactification. Math. Z. 71 (1959), 427–435.CrossRefGoogle Scholar
(5)Lorentz, G. G. and Keller, K.Über paare von Limitierungsverfahren. Math. Z. 68 (1958), 428–438.CrossRefGoogle Scholar
(6)Petersen, G. M.Summability and bounded sequences. Proc. Cambridge Philos. Soc. 55 (1959), 257–261.CrossRefGoogle Scholar
(7)Petersen, G. M.Consistent summability methods. J. London Math. Soc. 32 (1957), 62–65.CrossRefGoogle Scholar