Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Kuiper, Nicolaas H.
1967.
Algebraic equations for nonsmoothable 8-manifolds.
Publications mathématiques de l'IHÉS,
Vol. 33,
Issue. 1,
p.
139.


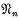 and Ω
and Ω