Research Article
The marriage lemma and large anonymous games with countable actions†
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 385-387
-
- Article
- Export citation
On the average number of divisors of quadratic polynomials
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 389-392
-
- Article
- Export citation
Quartic curves in characteristic 2
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 393-414
-
- Article
- Export citation
Geometry of quartic curves
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 415-423
-
- Article
- Export citation
Finite classical groups and multiplication groups of loops
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 425-429
-
- Article
- Export citation
Genus of nilpotent groups of Hirsch length six
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 431-438
-
- Article
- Export citation
McLain groups over arbitrary rings and orderings
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 439-467
-
- Article
- Export citation
Properties (V) and (w V) on C(Ω X)
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 469-477
-
- Article
- Export citation
Spectral characterization of the socle in Jordan–Banach algebras
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 479-489
-
- Article
- Export citation
Applications of the Birkhoff–Hopf theorem to the spectral theory of positive linear operators
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 491-512
-
- Article
- Export citation
Evaluation operators on the Bergman space†
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 513-523
-
- Article
- Export citation
Invariant domains and singularities
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 525-532
-
- Article
- Export citation
Zeros of linear combinations of orthogonal polynomials
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 533-544
-
- Article
- Export citation
On quantum SU(2) invariants and generalized bridge numbers of knots
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 545-557
-
- Article
- Export citation
Discrete subadditive functions as Gomory functions
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 559-574
-
- Article
- Export citation
Front matter
PSP volume 117 issue 3 Cover and Front matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
PSP volume 117 issue 3 Cover and Back matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b6
-
- Article
-
- You have access
- Export citation

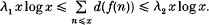
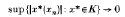
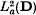 is the space of analytic functions
is the space of analytic functions 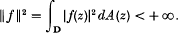
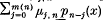 has
has 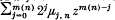 has
has 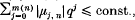 where
where