Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Schuster, Alexander
1997.
Sets of sampling and interpolation in Bergman spaces.
Proceedings of the American Mathematical Society,
Vol. 125,
Issue. 6,
p.
1717.
Dure, Peter
Schuste, Alexander
and
Vukotić, Dragan
2005.
Quadrature Domains and Their Applications.
Vol. 156,
Issue. ,
p.
131.
Nishio, Masaharu
Suzuki, Noriaki
and
Yamada, Masahiro
2008.
Interpolating Sequences of Parabolic Bergman Spaces.
Potential Analysis,
Vol. 28,
Issue. 4,
p.
357.
Nowak, K.
and
Pap, M.
2017.
Frames and Other Bases in Abstract and Function Spaces.
p.
355.


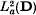 is the space of analytic functions
is the space of analytic functions 
