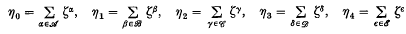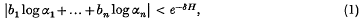Research Article
Bounded and invariant elements in 2-firs
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 1-12
-
- Article
- Export citation
On subgroups of amalgamated free products
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 13-23
-
- Article
- Export citation
A second anticommutant theorem for symmetric ternary algebras
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 25-52
-
- Article
- Export citation
Factorizations of completely positive matrices
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 53-58
-
- Article
- Export citation
Homology, Hilbert functions, and the conservation of number
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 59-70
-
- Article
- Export citation
Collapsing K × I to vertical segments
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 71-74
-
- Article
- Export citation
Automorphisms of metastably connected PL-manifolds
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 75-77
-
- Article
- Export citation
Compact operators and Banach algebras
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 79-85
-
- Article
- Export citation
Functions which operate on positive definite functions
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 87-97
-
- Article
- Export citation
Summability methods which include the Riesz typical means. I
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 99-106
-
- Article
- Export citation
Absolute total-effective (N, pn) means
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 107-122
-
- Article
- Export citation
Montel's theorem for subharmonic functions and solutions of partial differential equations
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 123-150
-
- Article
- Export citation
Integral means of subharmonic functions
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 151-152
-
- Article
- Export citation
The period equation for primes p congruent to 1 (mod 5)
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 153-155
-
- Article
- Export citation
An application of the Thue–Siegel–Roth theorem to elliptic functions
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 157-161
-
- Article
- Export citation
Some computations in the modular representation ring of a finite group
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 163-166
-
- Article
- Export citation
An iterative method to calculate the phases of Coulomb functions
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 167-173
-
- Article
- Export citation
Singularities of two-dimensional exterior solutions of the Helmholtz equation
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 175-188
-
- Article
- Export citation
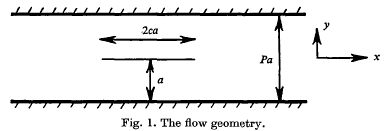
Two-dimensional flow past a flat plate in the presence of boundary walls
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 189-199
-
- Article
- Export citation
The scattering of surface waves by two submerged cylinders
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 201-215
-
- Article
- Export citation

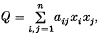 with
with 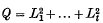
 (
(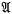 of
of 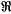 ,λ,μ) [Russell(14)], or Riemann-Cesàro summability (
,λ,μ) [Russell(14)], or Riemann-Cesàro summability (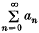 be a given infinite series with the sequence of its partial sums {
be a given infinite series with the sequence of its partial sums {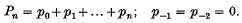
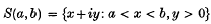


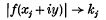



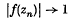

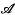 , ℬ,
, ℬ, 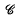 ,
, 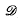 , ℰ, where g
, ℰ, where g