No CrossRef data available.
Compact operators and Banach algebras
Published online by Cambridge University Press: 24 October 2008
Extract
1. Introduction. Let X be a complex Banach space and let  (X) denote the Banach algebra of all bounded linear operators on X. In this paper we study subalgebras
(X) denote the Banach algebra of all bounded linear operators on X. In this paper we study subalgebras 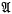 of
of  (X) that contain non-zero compact operators and that are Banach algebras with respect to some norm dominating the operator norm. Our main aim is to give conditions for the existence of minimal one-sided ideals in
(X) that contain non-zero compact operators and that are Banach algebras with respect to some norm dominating the operator norm. Our main aim is to give conditions for the existence of minimal one-sided ideals in 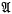 . Barnes ((l) Theorem 2·2) has shown that if every element of a semi-simple Banach algebra has countable spectrum then the algebra has minimal one-sided ideals. If, in particular,
. Barnes ((l) Theorem 2·2) has shown that if every element of a semi-simple Banach algebra has countable spectrum then the algebra has minimal one-sided ideals. If, in particular, 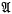 is a uniformly closed sub-algebra of the compact operators on X, then every element of
is a uniformly closed sub-algebra of the compact operators on X, then every element of 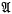 has countable spectrum by the Riesz–Schauder theory and so
has countable spectrum by the Riesz–Schauder theory and so 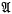 has minimal one-sided ideals. We extend this latter result by showing that if
has minimal one-sided ideals. We extend this latter result by showing that if 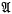 is a semi-simple uniformly closed subalgebra of
is a semi-simple uniformly closed subalgebra of  (X) that contains some non-zero compact operator, then
(X) that contains some non-zero compact operator, then 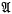 has minimal one-sided ideals. The proof depends heavily on the fact (see e.g. Bonsall (3)) that the spectral projection at a non-zero eigenvalue of a compact operator T belongs to the least closed subalgebra of
has minimal one-sided ideals. The proof depends heavily on the fact (see e.g. Bonsall (3)) that the spectral projection at a non-zero eigenvalue of a compact operator T belongs to the least closed subalgebra of  (X) that contains T. The uniform norm is quite critical for Bonsall's result, but we are able to give a mild generalization which leads to conditions for the existence of minimal one-sided ideals in subalgebras of
(X) that contains T. The uniform norm is quite critical for Bonsall's result, but we are able to give a mild generalization which leads to conditions for the existence of minimal one-sided ideals in subalgebras of  (X, Y,〈,〉) where (X, Y,〈,〉) are Banach spaces in normed duality.
(X, Y,〈,〉) where (X, Y,〈,〉) are Banach spaces in normed duality.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 69 , Issue 1 , January 1971 , pp. 79 - 85
- Copyright
- Copyright © Cambridge Philosophical Society 1971


