The kinetic stability properties of relativistic nonneutral electron flow in planar diode geometry are examined for extraordinary-mode perturbations about the self-consistent Vlasov equilibrium 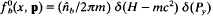 . Here, the cathode is located at x = 0; the anode is located at x = d the outer edge of the electron layer is located at
. Here, the cathode is located at x = 0; the anode is located at x = d the outer edge of the electron layer is located at 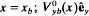 is the equilibrium flow velocity in the x-direction; n^b is the electron density at the cathode (x = 0); and
is the equilibrium flow velocity in the x-direction; n^b is the electron density at the cathode (x = 0); and 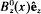 is the axial magnetic field, with
is the axial magnetic field, with 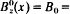 const. in the vacuum region (xb < x ≤ d). The extraordinary-mode eigenvalue equation, derived in a companion paper for low-frequency, long-wavelength perturbations, is solved exactly. This leads to a formal dispersion relation, which can be used to determine the complex eigenfrequency ω over a wide range of system parameters and wavenumber k in the y-direction. The formal dispersion relation is further simplified for
const. in the vacuum region (xb < x ≤ d). The extraordinary-mode eigenvalue equation, derived in a companion paper for low-frequency, long-wavelength perturbations, is solved exactly. This leads to a formal dispersion relation, which can be used to determine the complex eigenfrequency ω over a wide range of system parameters and wavenumber k in the y-direction. The formal dispersion relation is further simplified for 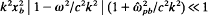 and
and  , assuming low-frequency perturbations about a tenuous electron layer with
, assuming low-frequency perturbations about a tenuous electron layer with 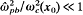 and
and 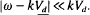 . Here,
. Here, 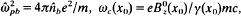 , and
, and 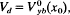 , where
, where 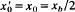 denotes the average equilibrium orbit, and [γ(x) − 1]mc2 is the average kinematic energy of an electron fluid element. The resulting approximate dispersion relation is solved numerically over a wide range of system parameters to determine the detailed dependence of stability properties on electromagnetic effects, layer thickness, and electron energy, as measured by
denotes the average equilibrium orbit, and [γ(x) − 1]mc2 is the average kinematic energy of an electron fluid element. The resulting approximate dispersion relation is solved numerically over a wide range of system parameters to determine the detailed dependence of stability properties on electromagnetic effects, layer thickness, and electron energy, as measured by  , and γb − 1, respectively. Here, γb = γ(xb) denotes the electron energy at the outer edge of the electron layer. As a general remark, it is found that increasing the electron energy (γb − 1), increasing the strength of electromagnetic effects
, and γb − 1, respectively. Here, γb = γ(xb) denotes the electron energy at the outer edge of the electron layer. As a general remark, it is found that increasing the electron energy (γb − 1), increasing the strength of electromagnetic effects 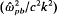 , and/or decreasing the layer thickness (xb/d) all have a stabilizing influence.
, and/or decreasing the layer thickness (xb/d) all have a stabilizing influence.