Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-28T01:12:17.506Z Has data issue: false hasContentIssue false
  • English
  • Français

Kinetic stability properties of relativistic nonneutral electron flow for low-frequency extraordinary-mode perturbations

Published online by Cambridge University Press:  09 March 2009

Ronald C. Davidson  and
Han S. Uhm
Ronald C. Davidson
Affiliation:
Plasma Fusion Center, Massachusetts Institute of Technology, Cambridge, MA 02139
Han S. Uhm
Affiliation:
Naval Surface Warfare Center, Silver Spring, MD 20903
Get access Rights & Permissions [Opens in a new window]

Abstract

The kinetic stability properties of relativistic nonneutral electron flow in planar diode geometry are examined for extraordinary-mode perturbations about the self-consistent Vlasov equilibrium 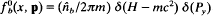. Here, the cathode is located at x = 0; the anode is located at x = d the outer edge of the electron layer is located at 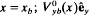is the equilibrium flow velocity in the x-direction; n^b is the electron density at the cathode (x = 0); and 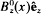is the axial magnetic field, with 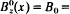const. in the vacuum region (xb < x ≤ d). The extraordinary-mode eigenvalue equation, derived in a companion paper for low-frequency, long-wavelength perturbations, is solved exactly. This leads to a formal dispersion relation, which can be used to determine the complex eigenfrequency ω over a wide range of system parameters and wavenumber k in the y-direction. The formal dispersion relation is further simplified for 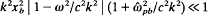and , assuming low-frequency perturbations about a tenuous electron layer with 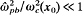and 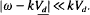. Here, 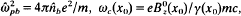, and 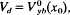, where 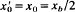denotes the average equilibrium orbit, and [γ(x) − 1]mc2 is the average kinematic energy of an electron fluid element. The resulting approximate dispersion relation is solved numerically over a wide range of system parameters to determine the detailed dependence of stability properties on electromagnetic effects, layer thickness, and electron energy, as measured by , and γb − 1, respectively. Here, γb = γ(xb) denotes the electron energy at the outer edge of the electron layer. As a general remark, it is found that increasing the electron energy (γb − 1), increasing the strength of electromagnetic effects 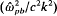, and/or decreasing the layer thickness (xb/d) all have a stabilizing influence.

Type
Research Article
Information
Laser and Particle Beams , Volume 7 , Issue 1 , February 1989 , pp. 85 - 109
Copyright
Copyright © Cambridge University Press 1989

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bekefi, G. 1982 Appl. Phys. Lett. 40, 2319.CrossRefGoogle Scholar
Briggs, R. J., Daugherty, J. D. & Levy, R. H. 1970 Phys. Fluids 13, 421.CrossRefGoogle Scholar
Buneman, O., Levy, R. H. & Linson, L. M. 1966 J. Appl. Phys. 37, 3203.CrossRefGoogle Scholar
Chang, C. L., Antonsen, T. M. Jr. & Drobot, A. T. 1984 Phys. Fluids 27, 2545.CrossRefGoogle Scholar
Chang, C. L. et al. 1984 Phys. Fluids 27, 2937.CrossRefGoogle Scholar
Chernin, D. & Lau, Y. Y. 1984 Phys. Fluids 27, 2319.CrossRefGoogle Scholar
Davidson, R. C. 1974 Theory of Nonneutral Plasmas (Benjamin, Reading, Mass.).Google Scholar
Davidson, R. C. & Uhm, H. S. 1982 Phys. Fluids 25, 2089.CrossRefGoogle Scholar
Davidson, R. C. & Tsang, K. T. 1984 Phys. Rev. 29, 488.CrossRefGoogle Scholar
Davidson, R. C., Tsang, K. T. & Swegle, J. A. 1984 Phys. Fluids 27, 2332.CrossRefGoogle Scholar
Davidson, R. C. 1984 Handbook of Plasma Physics—Volume 2: Basic Plasma Physics II (eds. Galeev, A. A. & Sudan, R. N.,—Elsevier, New York) pp. 768–816.Google Scholar
Davidson, R. C., McMullin, W. A. & Tsang, K. T. 1984 Phys. Fluids 27, 233.CrossRefGoogle Scholar
Davidson, R. C. & Tsang, K. T. 1985 Phys. Fluids 28, 1169.CrossRefGoogle Scholar
Davidson, R. C., Tsang, K. T. & Uhm, H. S. 1985 Phys. Rev. A32, 1044.CrossRefGoogle Scholar
Davidson, R. C. & Uhm, H. S. 1985 Phys. Rev. A32, 3554.CrossRefGoogle Scholar
Davidson, R. C. 1985a Phys. Fluids 28, 377.CrossRefGoogle Scholar
Davidson, R. C. 1985b J. Plasma Phys. 33, 157.CrossRefGoogle Scholar
Davidson, R. C. 1985C Phys. Fluids 28, 1937.CrossRefGoogle Scholar
Davidson, R. C. & Uhm, H. S. 1986 Phys. Fluids 29, 2273.CrossRefGoogle Scholar
Davidson, R. C. & Uhm, H. S. 1989 “Kinetic Extraordinary-Mode Eigenvalue Equation for Relativistic Nonneutral Electron Flow in Planar Geometry” Laser and Particle Beams, in press.CrossRefGoogle Scholar
Lau, Y. Y. 1984 Phys. Rev. Lett. 53, 395.CrossRefGoogle Scholar
Levy, R. H. 1965 Phys. Fluids 8, 1288.CrossRefGoogle Scholar
Mendel, C. W. Jr., Seidel, D. B. & Slutz, S. A. 1983 Phys. Fluids 26, 3628.CrossRefGoogle Scholar
Mendel, C. W., Jr, Swegle, J. A. & Seidel, D. B. 1985 Phys. Rev. A32, 1091.CrossRefGoogle Scholar
Miller, R. B. 1982 Intense Charged Particle Beams (Plenum, New York).Google Scholar
Orzechowski, T. J. & Bekefi, G. 1979 Phys. Fluids 22, 978.CrossRefGoogle Scholar
Petillo, J. J. & Davidson, R. C. 1987 Phys. Fluids 30, 2477.CrossRefGoogle Scholar
Rostoker, N. 1973 Particle Accelerators 5, 93.Google Scholar
Sprangle, P. & Kapetanakos, C. A. 1978 J. Appl. Phys. 49, 1.CrossRefGoogle Scholar
Swegle, J. & Ott, E. 1981a Phys. Rev. Lett. 46, 929.CrossRefGoogle Scholar
Swegle, J. & Ott, E. 1981b Phys. Fluids 24, 1821.CrossRefGoogle Scholar
Swegle, J. 1983 Phys. Fluids 26, 1670.CrossRefGoogle Scholar
Uhm, H. S. & Davidson, R. C. 1985 Phys. Rev. A31, 2556.CrossRefGoogle Scholar
Uhm, H. S., Davidson, R. C. & Petillo, J. 1985 Phys. Fluids 28, 2537.CrossRefGoogle Scholar
Vandevender, J. P. et al. , 1981 J. Appl. Phys. 52, 4.CrossRefGoogle Scholar
Vandevender, J. P. et al. 1985 Proc. International Conference on Plasma Physics and Controlled Nuclear Fusion Research(IAEA,Vienna,1984),Nucl. Fusion Suppl. 3, 59 and references therein.Google Scholar