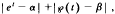Research Article
Rings with dual continuous right ideals
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 287-294
-
- Article
-
- You have access
- Export citation
Generalized products of weakly m — n compact spaces, I
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 143-151
-
- Article
-
- You have access
- Export citation
Twills on a given number of harnesses
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 1-15
-
- Article
-
- You have access
- Export citation
The free exact category on a left exact one
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 295-301
-
- Article
-
- You have access
- Export citation
Corrigendum
Order-bounded convergence structures on spaces of continuous functions: Corrigendum
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 16-17
-
- Article
-
- You have access
- Export citation
Research Article
Reducing two person, zero sum games with underlying symmetry
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 152-161
-
- Article
-
- You have access
- Export citation
A note on isometric immersions
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 162-166
-
- Article
-
- You have access
- Export citation
Latin squares with highly transitive automorphism groups
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 18-22
-
- Article
-
- You have access
- Export citation
The dilogarithm in algebraic fields
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 302-330
-
- Article
-
- You have access
- Export citation
Abelian Unipotent Subgroups of Finite Unitary and Symplectic Groups
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 331-344
-
- Article
-
- You have access
- Export citation
Amicable orthogonal designs of order eight
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 23-29
-
- Article
-
- You have access
- Export citation
On a class of near-rings
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 167-170
-
- Article
-
- You have access
- Export citation
Simultaneous approximation of et and ℘(t)
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 171-178
-
- Article
-
- You have access
- Export citation
Certain semigroups embeddabable in topological groups
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 30-39
-
- Article
-
- You have access
- Export citation
Abelian 2-subgroups of finite symplectic groups in characteristic 2
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 345-350
-
- Article
-
- You have access
- Export citation
Directed packings of pairs into quadruples
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 179-184
-
- Article
-
- You have access
- Export citation
Injective and projective Boolean-like rings
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 40-49
-
- Article
-
- You have access
- Export citation
On Modular Representation Algebras and a Class of Matrix Algebras
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 351-355
-
- Article
-
- You have access
- Export citation
Essential ideals, homomorphically closed classes and their radicals
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 356-363
-
- Article
-
- You have access
- Export citation
Weyl functions and the Ap condition on compact lie groups
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 185-192
-
- Article
-
- You have access
- Export citation

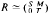 where
where