Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-23T14:17:03.294Z Has data issue: false hasContentIssue false
  • English
  • Français

Rings with dual continuous right ideals

Published online by Cambridge University Press:  09 April 2009

Saad Mohamed
Saad Mohamed
Affiliation:
Department of Mathematics Kuwait UniversityKuwait
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper the structure of rings with dual continuous right ideals is discussed. The main result is the following: If R is a ring with (Jacobson) radical nil, and all of its finitely generated right ideals are dual continuous, then 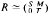where S is a finite direct sum of local rings each of which has its radical square zero, or is a right valuation ring, T is semiprimary right semihereditary ring, and M is an (S, T)-bimodule such that all of its finitely generated T-submodules are projective. A partial converse of this result is obtained: any matrix ring of the above type with M = 0 has all of its finitely generated right ideals dual continuous.

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 33 , Issue 3 , December 1982 , pp. 287 - 294
Copyright
Copyright © Australian Mathematical Society 1982

References

Faith, C. (1976), Algebra. II. Ring theory (Springer-Verlag, Berlin and New York).CrossRefGoogle Scholar
Goel, S. C. and Jain, S. K. (1976), ‘Semiperfect rings with quasi-projective left ideals’, Math. J. Okayama Univ. 19, 39–43.Google Scholar
Jain, S. K. and Singh, S. (1975), ‘Rings with quasi-projective left ideals’, Pacific J. Math. 60, 169–181.CrossRefGoogle Scholar
Koehler, A. (1971), ‘Quasi-projective and quasi-injective modules’, Pacific J. Math. 36, 713–720.CrossRefGoogle Scholar
Miyashita, Y. (1966), ‘Quasi-projective modules, perfect modules and a theorem for modular lattices’, J. Fac. Sci. Hokkaido Univ. 19, 86–110.Google Scholar
Mohamed, S. and Singh, S. (1977), ‘Generalization of decomposition theorems known over perfect rings’, J. Austral. Math. Soc. Ser. A 24, 496–510.CrossRefGoogle Scholar
Mohamed, S. and Müller, B. J. (1977), Decomposition of dual continuous modules, Lecture Notes in Math. 700, pp. 87–94. (Springer-Verlag, Berlin and New York).Google Scholar
Reda, F. A. (1978), On continuous and dual continuous modules (M.Sc. Thesis, Kuwait University).Google Scholar
Wu, L. E. T. and Jans, J. P. (1967), ‘On quasi-projective modules’, Illinois J. Math. 11, 439–448.CrossRefGoogle Scholar