No CrossRef data available.
Article contents
Simultaneous approximation of et and ℘(t)
Published online by Cambridge University Press: 09 April 2009
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Let t be any complex number different from the poles of a Weierstrass elliptic function ℘(z), having algebraic invariants. Then we estimate from below the sum 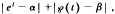 where α and β are algebraic numbers. The estimate is given in terms of the heights of α and β and the degree of the field Q(α, β), where Q is the field of rationals.
where α and β are algebraic numbers. The estimate is given in terms of the heights of α and β and the degree of the field Q(α, β), where Q is the field of rationals.
- Type
- Research Article
- Information
- Copyright
- Copyright © Australian Mathematical Society 1982
References
[1]Brownawell, W. D. and Masser, D. W., ‘Multiplicity estimates for analytic functions(I)’, J. Reine Angew. Math. 314 (1980), 200–216.Google Scholar
[2]Cijsouw, P. L. and Waldschmidt, M., ‘Linear forms and simultaneous approximations’, Compositio. Math. 34 (1977), 173–197.Google Scholar
[3]Masser, D. W., Elliptic functions and transcendence (Lecture Notes in Mathematics 437, Springer-Verlag, Berlin, 1977).Google Scholar
[4]Reyssat, E., ‘Approximation algébrique de nombres liés aux fonctions elliptiques et exponentielles’, Bull. Soc. Math. France (1980).CrossRefGoogle Scholar
[5]Saradha, K., Approximations of certain transcendental numbers, Thesis submitted to the University of Madras, 12 1980.Google Scholar


