Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-16T17:06:46.531Z Has data issue: false hasContentIssue false
  • English
  • Français

On Modular Representation Algebras and a Class of Matrix Algebras

Part of: Representation theory of groups

Published online by Cambridge University Press:  09 April 2009

J-C. Renaud
J-C. Renaud
Affiliation:
Department of Mathematics University of Papua New GuineaPapua New Guinea
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let G be a cyclic group of prime order p and K a field of characteristic p. The set of classes of isomorphic indecomposable (K, G)-modules forms a basis over the complex field for an algebra 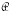p (Green, 1962) with addition and multiplication being derived from direct sum and tensor product operations.

Algebras 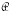n with similar properties can be defined for all n ≥ 2. Each such algebra is isomorphic to a matrix algebra Mn of n × n matrices with complex entries and standard operations. The characters of elements of 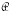n are the eigenvalues of the corresponding matrices in Mn.

MSC classification

Secondary: 20C20: Modular representations and characters
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 33 , Issue 3 , December 1982 , pp. 351 - 355
Copyright
Copyright © Australian Mathematical Society 1982

References

Abramovitz, M. and Stegun, I. (1972), Handbook of mathematical functions (Dover, New York).Google Scholar
Green, J. A. (1962), ‘The modular representation algebra of a finite group’, Illinois J. Math. 6, 607–619.CrossRefGoogle Scholar
Renaud, J-C. (1979), ‘The decomposition of products in the modular representation ring of a cyclic group of prime power order’, J. Algebra 58 (1), 1–11.CrossRefGoogle Scholar