In this note we shall be interested in the following problems.
Problem 1. Can IΔ0 ⊢ ∀x∃y > x(y is prime)?
Here I Δ0 is Peano arithmetic with the induction axiom restricted to bounded (i.e. Δ0) formulae.
Problem 2. Can IΔ0 ⊢ Δ0 PHP?
Here Δ0 PHP (Δ0 pigeonhole principle) is the schema
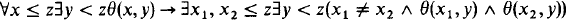
for θ ∈ Δ0, or equivalently in IΔ0, for a Δ0 formula F(x,y)
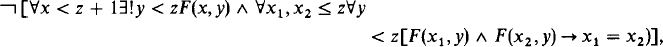
written 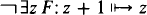 .
.
By obtaining partial solutions to Problem 2 we shall show that Problem 1 has a positive solution if IΔ0 is replaced by IΔ0 + ∀xx
log(x) exists.
Our notation will be entirely standard (see for example [3] and [4]). In particular all logarithms will be to the base 2 and in expressions like log(x), (1 + ε)x, etc. we shall always mean the integer part of these quantities.
Concerning Problem 2 we remark that it is shown in [5] that for k ∈ N and F ∈ Δ0,
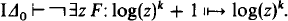
As far as we know this is the best result of this form, in that we do not know how to replace log(z)
k
by anything larger. However, as we shall show in Theorem 1, we can do much better if we increase the difference between the sizes of the domain and range of F.
In what follows let M be a countable nonstandard model of IΔ0, and let 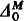 be those subsets of M defined by Δ0 formulae with parameters from M.
be those subsets of M defined by Δ0 formulae with parameters from M.
Theorem 1. For k ∈ N and
F ∈ Δ0,
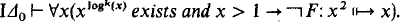
Here log0(x) = x, log
k + 1(x) = log(log
k
(x)).
Proof. To simplify matters, consider first the case k = 1. So assume M ⊨ a
log(a)
exists and 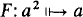 with
with 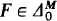 and a > 1. The idea of the proof is the following.
and a > 1. The idea of the proof is the following.